percorso di Giancarlo Cella
La relazione tra massa e curvatura dello spaziotempo descritta dalle equazioni di Einstein può produrre situazioni estremamente particolari, come i cosiddetti buchi neri. Per capirne la natura proviamo a chiederci come si modifica il diagramma spaziotemporale in Figura 4 in presenza di una massa (idealmente puntiforme) posta in r=0 .
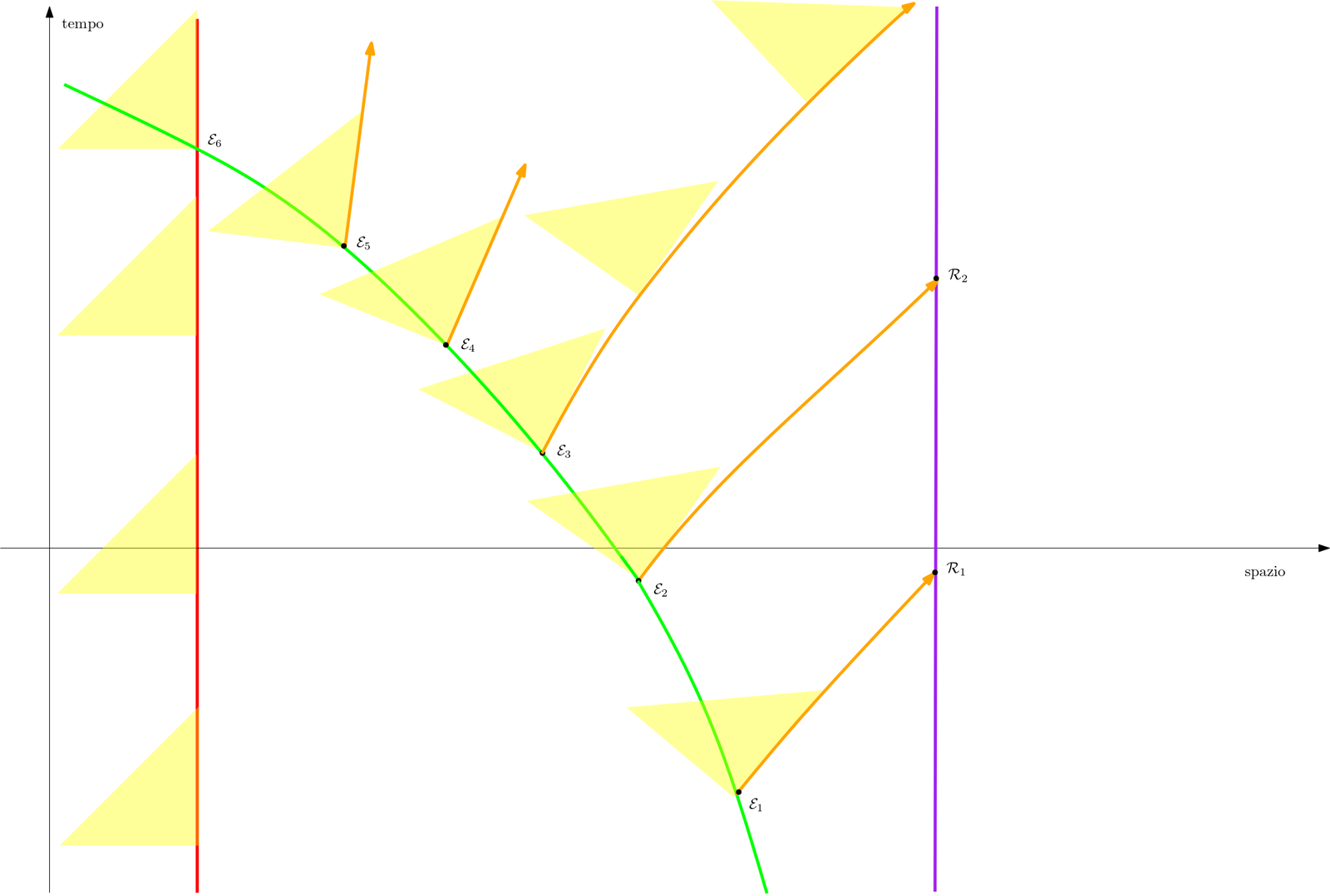
Figura 8: Coni luce e linee di universo in prossimità di una massa, concentrata idealmente in r=0 . I coni luce gialli sono ruotati per effetto della massa, in misura tanto maggiore quanto più ci si avvicina al centro. La linea verde corrisponde ad un corpo che sta cadendo verso il centro, la linea viola un corpo mantenuto a distanza costante da esso. In entrambi i casi le linee sono contenute nei coni luce associati ad ogni evento appartenente ad esse. Le linee arancioni rappresentano segnali luminosi (tangenti ai coni luce) emessi dal corpo verde e ricevuti dal corpo viola. Infine la linea rossa rappresenta l'orizzonte del buco nero descritto dal diagramma.
Orizzonti
Facciamo riferimento alla Figura 8. Come abbiamo visto, un campo gravitazionale causa una deflessione dei raggi luminosi, e questa sarà tanto maggiore quanto più ci avvicineremo alla massa. Possiamo rappresentare l’effetto disegnando i coni luce: questi tenderanno a ruotare in senso antiorario. La linea di universo verde rappresenta un corpo, ad esempio una nave spaziale, che sta cadendo verso la massa. Notiamo che, come deve essere, la linea resta sempre all'interno del cono luce. La linea di universo viola rappresenta un'altra nave spaziale, che si tiene a distanza costante molto grande dal centro. Da notare che a grandi distanze gli effetti gravitazionali sono trascurabili e quindi il cono luce ha la sua forma usuale aperta verso l'alto.
Supponiamo che l'astronave verde lanci verso l'esterno, a intervalli regolari, degli impulsi luminosi. Dato che questi si muovono alla velocità della luce, la loro linea di universo sarà in ogni punto tangente al cono luce.
L'effetto della dilatazione gravitazionale dei tempi si manifesta adesso in questo modo: dal punto di vista di un passeggero della navicella verde, cioè secondo il suo orologio, gli impulsi luminosi vengono inviati ad intervalli regolari, cioè in E1, E2 e così via. Se seguiamo la loro linea di universo vediamo invece che un passeggero della astronave viola li vedrà arrivare ad intervalli sempre maggiori: gli arrivi saranno R1, R2 e così via.
Ad una certa distanza dal centro, il cono luce sarà ruotato così tanto da avere un lato verticale: è chiaro che in queste condizioni niente potrà allontanarsi dal centro, neppure un raggio luminoso. Ed in effetti il segnale emesso in E6 non arriverà mai all'astronave viola.
Una volta che l'astronave verde avrà oltrepassato la linea rossa, non potrà più attraversarla nella direzione opposta ed anzi dovrà necessariamente cadere al centro. Dal punto di vista di un suo passeggero questo accadrà in un tempo ben definito.
Se ci fidiamo del principio di equivalenza inoltre il passeggero non dovrebbe avvertire niente di speciale durante la sua caduta libera.
In realtà sappiamo che questo non è esattamente vero, e che gli effetti gravitazionali inizieranno a “stirare” l'astronauta nella direzione radiale. Questi effetti diventeranno sempre più intensi avvicinandosi al centro, fino a ucciderlo e distruggere il suo corpo.
Dal punto di vista di un osservatore sull'astronave viola la storia è piuttosto differente: a causa della dilatazione del tempo, l'astronave verde sembrerà muoversi sempre più lentamente, fino a fermarsi alla distanza corrispondente alla linea rossa.
In realtà prima che questo accada, a causa dello spostamento verso il rosso, l'immagine dell'astronave e i segnali da essa inviati arriveranno a frequenze sempre più basse.
Se l'astronave è veramente verde, inizierà a cambiare colore per diventare gialla, poi rossa, quindi invisibile nell'infrarosso e in frequenze ancora più basse.
La linea rossa, che in realtà è la superficie sferica posta intorno alla massa, è l'orizzonte di un buco nero. Si trova ad una distanza dal centro direttamente proporzionale alla massa stessa, detta raggio di Schwarzschild Rs , e la situazione descritta richiede che tutta la massa sia contenuta al suo interno. Per dare un'idea:
- Il raggio di Schwarzschild corrispondente alla massa della Terra è di circa 9 millimetri. Chiaramente la massa della Terra è ben lontana dall'essere contenuta al suo interno, e in effetti la Terra non è un buco nero. Per trasformarla in esso, sarebbe necessario comprimere tutta la sua massa all'interno di Rs.
- Il raggio di Schwarzschild del Sole è di circa 3 kilometri. Anche in questo caso non abbiamo un buco nero.
- Se una massa sufficientemente grande viene concentrata a densità abbastanza elevate si può formare un buco nero. Si ha evidenza diretta e indiretta di buchi neri di masse stellari (da circa 3 masse solari fino a qualche centinaio di masse solari) e di buchi neri supermassicci, presenti al centro delle galassie e con masse di milioni o miliardi di masse solari.
Un buco nero è caratterizzato dal suo orizzonte che può essere attraversato dall'esterno verso l'interno ma mai in verso opposto.
Un modo intuitivo per descrivere quanto accade è rendersi conto che in prossimità di ogni massa possiamo definire la velocità di fuga. Ad esempio la velocità di fuga dalla superficie terrestre è di 40320 kilometri all'ora: questo significa che se vogliamo lanciare un oggetto verso l'alto in modo da farlo sfuggire all'attrazione del pianeta dobbiamo superare questa velocità (trascurando gli attriti con l’aria).
La velocità di fuga aumenta proporzionalmente alla radice quadrata della massa del pianeta o della stella ed è inversamente proporzionale alla radice quadrata della distanza dal centro. Per confronto, la velocità di fuga dalla superficie del Sole è di 2222280 kilometri all'ora.
Abbastanza vicino ad una massa sufficientemente grande la velocità di fuga può superare quella della luce: in questo caso non sarà possibile sfuggire in nessun modo all'attrazione.
Da quanto detto sembra seguire che tutta la massa di un buco nero, interna all'orizzonte, debba finire concentrata in un punto a r=0 . In realtà non disponiamo ancora degli strumenti teorici necessari per descrivere la struttura del centro di un buco nero: questo richiederebbe una teoria quantistica della gravitazione, che ad oggi non è ancora stata definita.
 Buchi neri rotanti
Buchi neri rotanti
La descrizione fatta nella sezione precedente riguarda una classe particolare di buchi neri, detti di Schwarzschild. Si tratta del tipo più semplice, che è completamente descritto dalla sua massa.
Si tratta di una delle soluzioni esatte delle equazioni di Einstein menzionate precedentemente.
Una soluzione più complicata descrive i cosiddetti buchi neri di Kerr: in questo caso oltre alla massa deve essere specificato il momento angolare, e possiamo interpretare questi oggetti come buchi neri rotanti.
Ci si attende che si tratti del tipo più frequente in natura. Un buco nero può infatti formarsi dal collasso di una stella di massa abbastanza grande, oppure dalla fusione di coppie di buchi neri o stelle a neutroni. Sistemi di questo tipo possiedono generalmente una rotazione (momento angolare) che si ritrova nel buco nero finale.
La rotazione genera una serie di fenomeni nuova: in particolare la struttura dei coni luce attorno al buco nero può essere distorta in modo tale da impedire ad un oggetto (ad esempio la solita astronave) di rimanere fermo, per quanto potenti possano essere i suoi motori.
Possiamo visualizzare la situazione immaginando che il buco nero in rotazione trascini lo spaziotempo attorno a se: quando la velocità di trascinamento è maggiore della velocità della luce non può essere contrastata da nessun corpo. In realtà questo effetto di trascinamento è presente, sempre secondo la Relatività Generale, attorno a un corpo rotante qualsiasi, seppure in misura molto minore, ed è detto effetto Lense–Thirring.