Come vincere il titolo di gomitolo dimensionale

Dal momento che non è quindi concesso esaminare sperimentalmente questi "gomitoli"...possiamo cercare di evincer come la natura abbia deciso di compattificare le dimensioni extra? La risposta viene proprio dal mondo che ci circonda...

Una delle caratteristiche di base risulta esser la simmetriadello spazio.

Ogni particolare forma ha diverse simmetrie: così un cubo è invariante rispetto a traslazione ed a rotazioni di 90 gradi…. Un cono è invariante rispetto a rotazioni solo attorno al suo asse. Una sfera è il solido con la maggior simmetria…

Anche ai possibili spazi di compattificazione sono associate diverse simmetrie.  Ciò dovrebbe riflettersi in natura: ad ogni simmetria risulta infatti esser associata nel nostro mondo una particolare proprietà (principio di conservazione): ad esempio la teoria dell’elettromagnetismo è invariante per “rotazioni” in uno spazio “interno”… da qui deriva il principio di conservazione della carica elettrica.

Partendo dall'analisi della realtà, ossia vedendo quanti sono i principi di conservazione noti, si può cercare di stabilire quindi il grado di simmetria dei “gomitoli” spaziali.

Inizialmente si pensava che le dimensioni extra potessero esser compattificate in un toroa 6 dimensioni… Tuttavia tale spazio risultava esser “troppo simmetrico” rispetto a ciò che si riscontrava in natura…

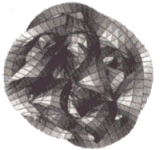
Gli spazi aventi caratteristiche tali da adattarsi al meglio alla “nostra realtà” provengono dalla matematica: sono spazi a 6 dimensioni noti come “spazi di Calabi-Yau”.

Esempio di un gomitolo dimensionale: uno dei possibili spazi di Calabi-Yau

 (immagine tratta da l'Universo Elegante, Brian Greene)