percorso di Silvia Miozzi
Per poter osservare un oggetto è necessario illuminarlo con una sorgente di fotoni e, se vogliamo distinguerne i dettagli, la lunghezza d’onda della luce deve essere comparabile con le dimensioni dell’oggetto stesso.
Per osservare i dettagli di un sistema su scala atomica è quindi necessario utilizzare come sonda fotoni che abbiano lunghezza d’onda λ comparabili con le dimensioni dell’atomo (λ <10-10 m). Poiché in natura non esistono fotoni di questo tipo, per farlo si sfrutta la proprietà che hanno le particelle subatomiche di sviluppare proprietà ondulatorie quando si muovono ad alta velocità. Questo principio, il dualismo onda-particella, è uno dei fondamenti della Meccanica Quantistica che, insieme alla relatività ristretta, è l’altra teoria fondamentale per esplorare i fenomeni subatomici.
Secondo il principio di De Broglie una particella con impulso p può essere vista come un’onda elettromagnetica di lunghezza d’onda λ
\[p=\frac{h}{\lambda }\]
dove h = 6,62607015\(\cdot\)10-34 J s è la costante di Planck.
Una particella può essere quindi utilizzata come sonda e più è alta la sua energia maggiore è l’impulso, minore è la lunghezza d’onda e maggiori saranno i dettagli che possono essere esaminati. Per questo motivo la fisica delle particelle elementari è detta anche fisica delle alte energie.
Le particelle lanciate contro un bersaglio, sono capaci di penetrare nel campo di forze nucleari che si trova nel cuore dell'atomo, disintegrandolo e permettendoci di studiarne i componenti. In questi urti violentissimi vengono anche create nuove particelle perché l’energia può trasformarsi in materia.
|
\[m=\gamma m_{0}\] dove m0 è la massa a riposo della particella
\[\gamma =\frac{1}{\sqrt{1-\beta ^{^{2}}}}\] \[\beta =\frac{v}{c}\]
\[E^{2}=p^{2}c^{2}+m_{0}^{2}c^{4}\] che rappresenta la relazione tra energia e impulso Si può arrivare alla stessa relazione definendo nello spazio 4-dimensionale la quantità P = [E/c, p ] = [mγc, mγv ] quadrivettore energia-impulso Il prodotto di un vettore per se stesso rappresenta un invariante nello spazio tridimensionale, questo è vero anche nello spazio quadrimensionale \[\sqrt{PP}= \sqrt{\frac{E^{2}}{c^{2}}-p^{2}}= \sqrt{(m\gamma c)^{2}-(m\gamma v)^{2}}= m\gamma \sqrt{1-\beta ^{2}c}= mc\] Da cui si ricava Per una particella ultrarelativistica |
Al di sopra di una certa energia la velocità della particella diventa praticamente costante e prossima a quella della luce. L’energia delle particelle accelerate si misura in electron Volt (eV) 1eV é l’energia cinetica acquistata da un elettrone sottoposto ad una differenza di potenziale di 1 Volt. Un elettrone diventa relativistico quando la sua energia è maggiore di 1 MeV (106 eV) mentre un protone ha bisogno di un’energia 1000 volte più alta.
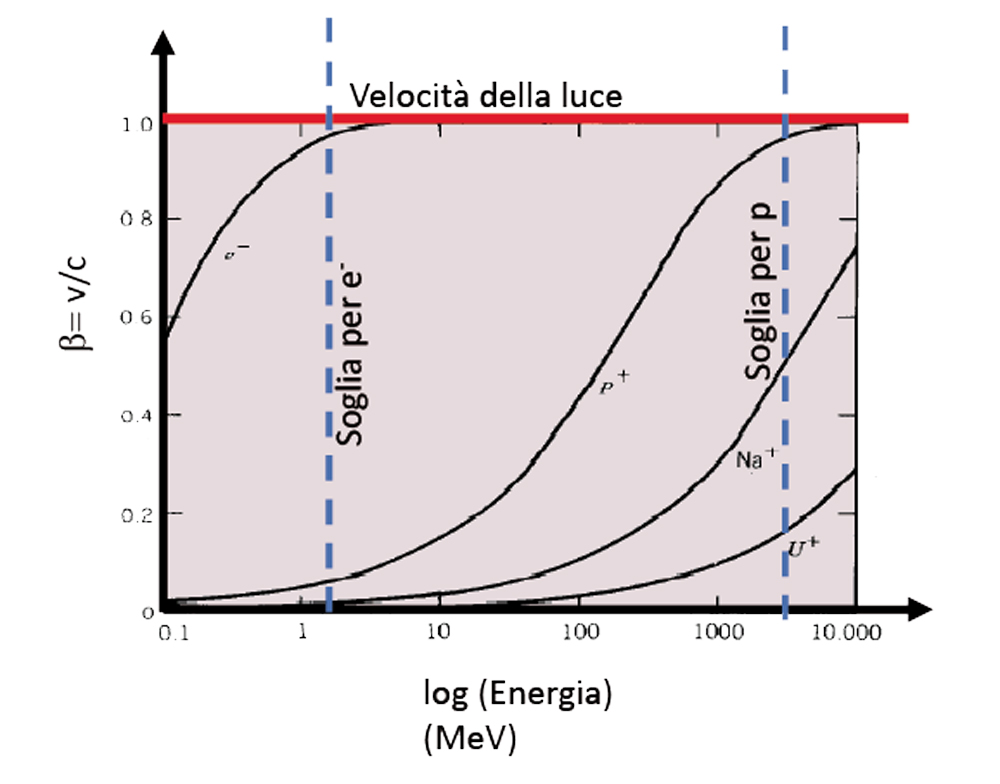
figura 1
Al momento l’acceleratore più potente è il Large Hadron Collider (LHC) al CERN di Ginevra con un’energia di 14 TeV (1012 eV) nel centro di massa.