Strappare e ricucire lo spazio

Quando pensiamo ad uno strappo siamo soliti immaginare un pezzo di carta, di stoffa... che perde la propria trama lineare generando un buco. Estendere il concetto allo spazio che ci circonda, alle "dimensioni spaziali" risulterà un po' arduo. 

Tuttavia alcuni ricercatori, usando la matematica come forbici e ago, notarono come strappando uno spazio di Calabi-Yau in un determinato punto e successivamente chiudendo il foro attraverso precisi procedimenti matematici, si giungesse ad  un nuovo spazio di Calabi-Yau.

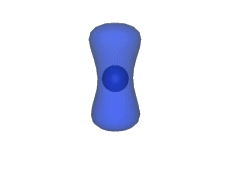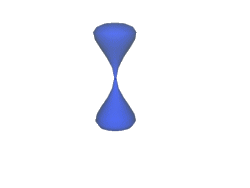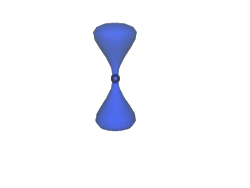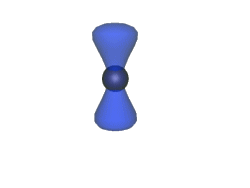
All'interno di uno spazio di Calabi-Yau possono essere contenute delle "sfere" in grado di contrarsi sempre di più, fino a ridursi ad un punto.In questo modo nella regione di spazio interessata si creerà un foro.La superficie sarà "rattoppata" quando la sfera ricomincerà a gonfiarsi.

A questo procedimento di "taglia e cuci" viene dato il nome di flop, e lo spazio "rattoppato"  risulta esser topologicamente differente da quello iniziale. Non riuscirete mai ad ottenere questo spazio da uno spazio di partenza senza almeno strapparlo una volta. 

Naturalmente queste operazioni hanno una loro consistenza nell'"universo matematico". Ma se identifichiamo lo spazio che ci circonda, come basato su spazi di Calabi-Yau, perchè  mai questo processo non potrebbe avvenire anche nel "nostro universo"? Probabilmente anche ora da qualche parte le dimensioni si stanno logorando... Come interpretare questi risultati in relazione alla trama lineare dello spazio prevista dalla Relatività Generale?