Incontri tra stringhe

Sebbene in questo strano mondo sembrerebbero esistere stringhe in grado di attraversarsi come se nulla fosse, in generale due stringhe che si incontrano interagiscono. 

Le stringhe aperte "scontrandosi" possono unire i propri estremi, o incrociarsi, come nel crossing-over, scambiandosi frammenti reciprocamente. 

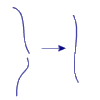
Stringhe chiuse possono invece fondersi in una nuova cordicella, determinando un foglio d'uni- verso topologicamente simile ad un cilindro con 2 estremità aperte. 

Tuttavia, come accade  successivamente ad  un processo di annichilazione, la nuova stringa potrebbe "sdoppiarsi " nuovamente in 2 stringhe. Nel foglio d'universo sarebbero presenti ora 4 estremità aperte

I-le due stringhe interagiscono

II-si crea una  nuova stringa

III-si "rimaterializzano" le 2 stringhe

A loro volta le stringhe potrebbero riinteragire, e la nuova stringa ridividersi... generando "un buco" nel foglio, e rendendolo topologicamente simile ad una ciambella.

IV- le due stringhe interagiscono nuovamente

V-si forma una nuova stringa

VI-la stringa si ridivide

Queste fusioni e sdoppiamenti potrebbero avvenire in diversi modi. Fortunatamente però nell'analisi delle interazioni non interessa tanto la geometria, quanto la topologia del foglio dell'universo descrivente il processo: non è importante cioè la precisa forma, ma proprietà come il numero di buchi presenti...Il che semplifica la situazione!

Scompaiono gli infiniti!

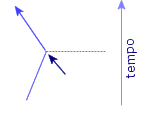
E questo non è l'unico risultato positivo.  Come si nota nei fogli d'universo, avendo le stringhe una propria estensione a differenza delle particelle elementari, le interazioni non avvengono in un preciso punto dello spazio tempo. 

<-interazione tra particelle

Tale inconveniente nelle teorie "particellari" porta infatti all'origine di infiniti che spuntano nelle equazioni creando non pochi problemi e rendendole talvolta irrisolvibili. Ostacoli superati grazie agli appena 10^-33 cm delle stringhe.