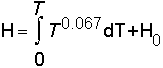Nella domanda, che riguarda le rappresentazioni delle trasformazioni politropiche Nella domanda, che riguarda le rappresentazioni delle trasformazioni politropiche  in funzione delle variabili di stato e delle funzioni di stato, il nostro web-nauta dice di averle trovate sempre e solo in diagrammi delle coppie di variabili termodinamiche p, V, T. In realtà, ci sono anche le altre rappresentazioni desiderate, ma sono per lo più contenute nei testi di fisica tecnica o di macchine termodinamiche. Questo è comprensibile perchè nei testi di termodinamica di base una rappresentazione come quella della fig 1 serve a definire una trasformazione politropica. Infatti la definizione di trasformazioni di questo tipo si basa su condizioni che vengono imposte alle variabili di stato in funzione delle variabili di stato e delle funzioni di stato, il nostro web-nauta dice di averle trovate sempre e solo in diagrammi delle coppie di variabili termodinamiche p, V, T. In realtà, ci sono anche le altre rappresentazioni desiderate, ma sono per lo più contenute nei testi di fisica tecnica o di macchine termodinamiche. Questo è comprensibile perchè nei testi di termodinamica di base una rappresentazione come quella della fig 1 serve a definire una trasformazione politropica. Infatti la definizione di trasformazioni di questo tipo si basa su condizioni che vengono imposte alle variabili di stato
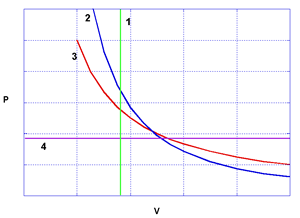 Figura 1 Rappresentazione delle curve di trasformazioni politropiche, nel piano p V, Figura 1 Rappresentazione delle curve di trasformazioni politropiche, nel piano p V, per un gas ideale e per particolari valori di n: curva 1 per n = ∞ -> isocora; curva 2
per n = g = Cp/Cv -> adiabatica; curva 3 per n = 1 -> isoterma; curva 4 per n = 0 -> isobara.
Si definisce politropica una trasformazione nella quale le variabili di stato p e V sono vincolate dall’equazione: pVn = cost accompagnata dalla condizione che il calore specifico deve rimanere costante durante la trasformazione e, come il richiedente ha mostrato di conoscere bene, specificando per n alcuni valori sigificativi si ottengono le politropiche classiche rappresentate in fig 1. Tali curve si riferiscono, è essenziale tenerlo presente, a trasformazioni reversibili, le sole che possono essere rappresentate da traiettorie nello spazio delle variabili di stato.
Naturalmente, le trasformazioni p = cost, V = cost, T = cost , che sono politropiche particolari (corrispondenti ai valori di n rispettivamente eguali a ∞, 0, 1), sono rappresentate da rette normali agli assi delle variabili corrispondenti e sono valide per tutti i sistemi termodinamici possibili. Per le altre trasformazioni, invece, si possono tracciare le varie curve solo conoscendo la funzione di stato del sistema considerato. Per esempio la curva di una trasformazione isoterma è l' iperbole di fig.1, solo per un gas che abbia come equazione di stato pV = cost T che è appunto quella dei gas ideali. I vari diagrammi sono usati per poter “vedere” immediatamente la grandezza fisica che interessa, per es. nel piano pV l’area compresa tra la curva di una qualsiasi trasformazione e la ascissa V tra i valori del volume iniziale e quello finale dà direttamente il lavoro compiuto (o assorbito) dal sistema sull’esterno.
Per ritornare al nocciolo della domanda, si capisce come non esistano “le leggi base per graficare una trasformazione politropica nei piani T-H ecc..” Quello che bisogna fare (quindi un metodo non una legge) è considerare la rappresentazione desiderata, il sistema in oggetto, la sua equazione di stato, la funzione termodinamica che interessa e ricavare analiticamente la relazione che si vuole graficare. E’ facile comprendere la difficoltà di queste operazioni. Le equazioni di stato dei sistemi reali sono o molto complicate o approssimate per es con delle serie (pensiamo ai gas reali) e quindi, esclusi pochissimi casi si procede per approssimazioni numeriche. Per questo attualmente i problemi si sono molto attenuati con l’aiuto dei grandi calcolatori che hanno potenziato in maniera impressionante i calcoli numerici. Poiché, fortunatamente, il richiedente dichiara il suo interesse per i gas ideali possiamo dire che le difficoltà sono minime per la semplicità dell’equazione di stato, anzi il ricavare le varie relazioni può essere un divertente esercizio. Noi faremo vedere come si procede per ricavare, ad esempio, le curve dell’entalpia H in funzione di T per un gas ideale nel caso di alcune politropiche.
Per definizione:
l’ entalpia è H = U + pV mentre l’ equazione di stato per una mole è pV = RT
1) isoterma: dT=0
ricordando che l’energia interna U di un gas ideale. è funzione solo di T si vede immediatamente che a T = cost anche H = cost Differenziamo ora le due relazioni: dH = dU + pdV + Vdp ; pdV + Vdp = RdT
2) isocora: dV = 0
dH = dU + Vdp; Vdp = RdT ma per un gas ideale dU = dQ - pdV = CvdT ed essendo dQ = CvdT dH = CvdT + RdT = CpdT e, integrando H = ? CpdT = Cp T + Ho (la costante Ho è collegata all’esistenza di Uo, l’energia che, per motivi quantistici, tutti i sistemi hanno allo zero assoluto )
3) isobara: dp = 0
dH = dU + pdV; dQ - pdV + pdV = CvdT quindi H = *CvdT = Cv T + Ho
4) adiabatica: dQ = 0
quindi dU = - pdV ; dH = Vdp
dalle equazioni delle adiabatiche 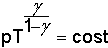
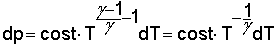
 e dalla e dalla 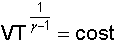
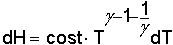 infine per un gas monoatomico (Υ=cp/cv=1.6666) infine per un gas monoatomico (Υ=cp/cv=1.6666)
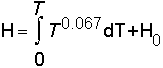
Nella seguente figura sono tracciate le varie curve di H per le politropiche considerate.
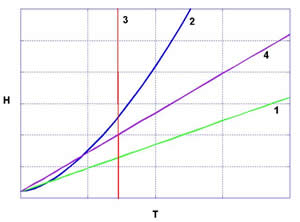
Figura 2 Rappresentazione dell’ entalpia di un gas ideale
in funzione di T per le stesse politropiche di fig 1. 1 isobara,
2 adiabatica, 3 isoterma, 4 isocora.
Come abbiamo detto, per i sistemi reali i calcoli sono più complicati, ma molte volte fondamentali per poter studiare il funzionamento dei vari sistemi termodinamici, per esempio si possono citare le curve delle politropiche del vapor d’acqua (macchine a vapore, turbine ecc.) dei gas di combustione per i vari tipi di motore a scoppio ecc. L’applicazione, anche dettagliata, dello studio delle politropiche si può trovare su molti buoni testi di fisica tecnica o teoria delle macchine dei corsi di Ingegneria.
Ivo Modena – Fisico
|


 Figura 1 Rappresentazione delle curve di trasformazioni politropiche, nel piano p V,
Figura 1 Rappresentazione delle curve di trasformazioni politropiche, nel piano p V,