Chiacchiere di Fisica

Produrre antimateria per distruggere il mondo

Chiacchiere di fisica di Stefano Marcellini
Produrre antimateria per distruggere il mondo
Nel romanzo Angeli e Demoni di Dan Brown un complotto mira a distruggere il Vaticano utilizzando dell’antimateria prodotta al Cern di Ginevra. Romanzi a parte: veramente al Cern producono antimateria? E è pericoloso?
Al Cern, effettivamente, fra i vari esperimenti ce ne sono alcuni che producono antimateria. O meglio, producono singoli atomi di anti-idrogeno per studiarli, e per capire se hanno qualche proprietà che li distingua dai normali atomi di idrogeno, tipo – metti caso – che cadano in modo diverso sotto l’effetto del campo gravitazionale. Dal punto di vista scientifico sarebbe una scoperta fantastica!
Ma sarebbe possibile produrre grandi quantità di antimateria da costituire un pericolo? Per rispondere a questa domanda basti dire che in tutta la storia della fisica delle particelle al Cern, la quantità di antimateria prodotta finora è una decina di miliardesimi di grammo, appena sufficienti per alimentare una lampadina da 60 W per 4 ore. Un po’ poco per distruggere il mondo!

Cosa hanno in comune un bagnino e un raggio di luce?
Chiacchiere di fisica di Stefano Marcellini
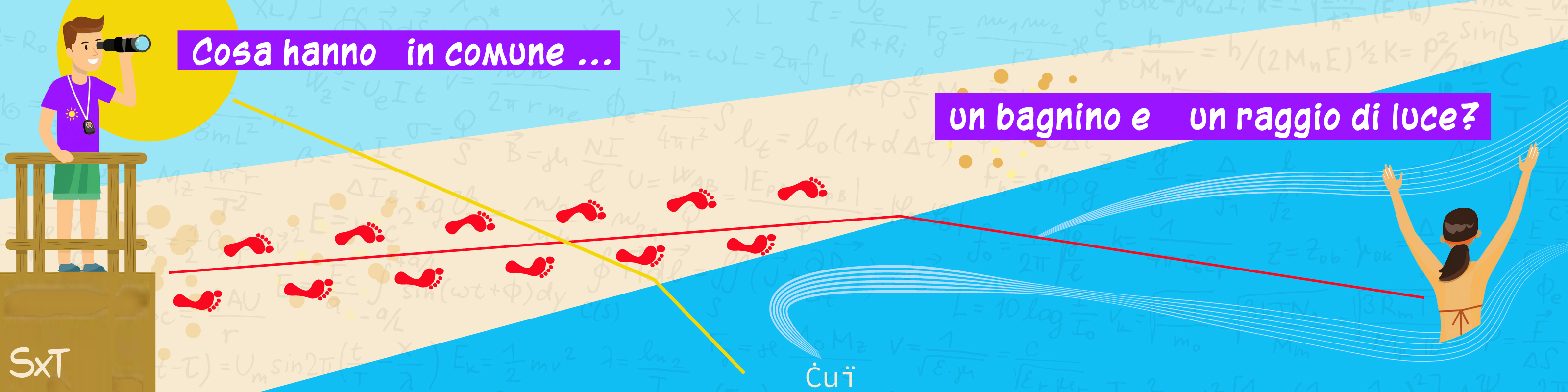
Cosa hanno in comune un bagnino e un raggio di luce?
Questo esempio purtroppo non l’ho inventato io, ma Richard Feynman, uno che di fisica ne sapeva a pacchi, e la sapeva anche raccontare.
Siete un bagnino: state lì sulla torretta, e all’improvviso vedete qualcuno in mezzo al mare, in diagonale rispetto alla vostra posizione, che sta annegando. Dovete intervenire nel minor tempo possibile: che percorso seguireste?
Molti risponderanno: “la linea retta, è il percorso più breve!
Però attenzione! Deve essere il percorso temporalmente più breve! E quindi sceglierete di percorrere un tragitto più lungo sulla sabbia, dove siete veloci, e più corto in mare, dove siete molto più lenti. Il risultato sarà una linea spezzata che rappresenta il compromesso migliore fra sabbia e mare, in modo da minimizzare il tempo impiegato.
La luce fa esattamente la stessa cosa quando deve andare da A a B attraversando due mezzi in cui la sua velocità di propagazione è diversa. La luce sceglie sempre il percorso più veloce possibile, come il bagnino. Il fenomeno che ne scaturisce si chiama “rifrazione”.

Se E=mc2 perchè non ci trasformiamo in energia
Chiacchiere di fisica di Stefano Marcellini
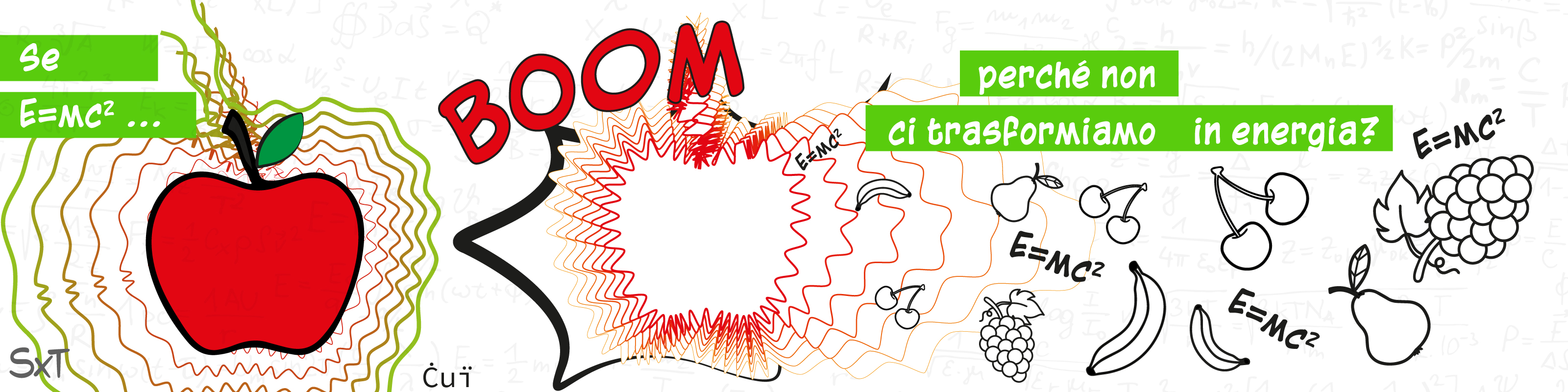
Se E=mc2, perché non ci trasformiamo in energia?
La teoria della relatività afferma che massa ed energia sono quantità equivalenti, legate dalla famosa formula E=mc2, dove m, la massa a riposo di un corpo, equivale a una energia E. E siccome quel c al quadrato è un numero bello grande, il risultato è anche un bel po’ di energia. E allora perché non ci trasformiamo in un lampo di raggi gamma? Cosa lo impedisce?
Fortunatamente la Natura ha imposto dei lucchetti: proprietà della materia che non possono semplicemente sparire senza violare principi di conservazione sacrosanti, tipo la carica elettrica o altre caratteristiche che hanno a che fare con il mondo nucleare o subnucleare.
Quindi, sebbene dal punto di vista prettamente energetico alla formula E=mc2 non sembrerebbe vero di entrare in azione, gli sbarramenti che la Natura ha al suo interno impediscono che ciò accada spontaneamente. Per fortuna! Altrimenti non avreste potuto leggere questo post, visto che non sareste esistiti né voi né il suo autore.

Viaggiare indietro nel tempo?

Chiacchiere di fisica di Stefano Marcellini
Viaggiare indietro nel tempo?
Vorreste fare un viaggio indietro nel tempo, e vedere gli egizi che costruivano le piramidi? O i T-Rex che scorrazzavano? E rivedere il Big Bang?
Mentre non c’è verso di rivedere gli egizi o i dinosauri, noi possiamo realmente vedere l’Universo a ridosso del Big Bang: basta solo guardare distante! Quando guardiamo un oggetto, infatti, lo vediamo non come è in quel momento, ma come era quando la luce che ci arriva agli occhi lo aveva illuminato e con esso aveva interagito, o da esso era stata emessa. Con la Luna corrisponde a poco più di un secondo, con il Sole 8 minuti, con le galassie distanti, miliardi di anni.
Grazie a questa incredibile macchina del tempo scopriamo che nel passato remoto le galassie erano mediamente diverse da quelle attuali. Non dobbiamo ipotizzare l'evoluzione dell’Universo: la vediamo!
E scopriamo che oltre 13 miliardi di anni fa le galassie neanche esistevano, e lo spazio era permeato da onde elettromagnetiche che ci fotografano un universo caldo e uniforme, con solo alcune tenui increspature di densità. In quelle increspature c’è il germe di tutto ciò che verrà poi. In quelle increspature ci siamo anche noi.

Grosso guaio a Lottolandia

Chiacchiere di fisica di Stefano Marcellini
Grosso guaio a Lottolandia
Nella Repubblica di Lottolandia il gioco del Lotto è più che una mania nazionale, è una vera e propria istituzione. Qualunque cittadino, salvo rare eccezioni, non manca mai di giocare almeno una schedina alla settimana, con la speranza di azzeccare la combinazione giusta, fosse solo un semplice ambo. Il gioco del lotto, insomma, è il motore economico e sociale di Lottolandia.
E di pari passo pullulano naturalmente i trattati scientifico-matematici per prevedere quali saranno le combinazioni più probabili dei numeri in uscita. Tra questi primeggiano gli studi sui cosiddetti "ritardi", che in base a questi ultimi prevedono la probabilità di estrazione di ogni numero. Perché è naturale che un numero, più è in ritardo la sua estrazione, più diventi probabile che esca! Purtroppo alcuni negazionisti - gente ai margini della società - continuano ad affermare che puntare sui ritardi dei numeri è una sciocchezza bella e buona, perché la probabilità di uscita di un numero è del tutto indipendente dal suo ritardo, dato che i numeri non hanno ricordi. Ma nonostante queste rare voci fuori dal coro, per lo più opera di disinformatori, puntare sui ritardi dei numeri è una prassi consolidata a Lottolandia.
In questo momento il numero che sta monopolizzando l'attenzione di tutti i cittadini di Lottolandia (esclusi quei pochi ribelli che non giocano al lotto e stupidamente se ne vantano pure) è il 74, che non esce da ben 234 settimane sulla ruota di Dumb. Un ritardo del genere a Lottolandia non si era mai visto. Ogni settimana la quasi totalità della popolazione punta sul 74 sulla ruota di Dumb, confortata dalle precise previsioni matematiche basate sul suo enorme e inusuale ritardo, che rende ovviamente altissima la probabilità della sua imminente uscita.
Ultimamente però un evento imprevisto ha letteralmente sconvolto quella terra tranquilla. A causa della crisi economica, che ha colpito anche l'economia di quel piccolo stato, il ministro del Lotto e Gratta e Vinci si è visto costretto a tagliare sul numero delle ruote, portandole dalle 200 che erano a 50, unificando assieme fra loro più ruote diverse. E il caso ha voluto che la ruota di Dumb, nella quale il numero 74 è in ritardo da 234 settimane, sia stata unificata con la ruota di Twerp. Solo che - piccolo problema - nella ruota di Twerp il 74 è uscito giusto la settimana scorsa!
Lo sconcerto della popolazione a questo punto è più che comprensibile. È meglio puntare tutto sul 74, dato che questo numero non esce su quella ruota da 234 settimane, oppure conviene puntare su tutto meno che sul 74, che sulla stessa ruota (adesso sono proprio la stessa ruota!) è uscito pochi giorni fa? Conterà di più che è appena uscito, o che non esce da 234 settimane? E mentre gli esperti del Lotto stanno sviluppando nuovi complessi calcoli matematici per dipanare la questione, come l'asino di Buridano, che di fronte alla scelta su quale mucchio di fieno mangiare morì di fame, i cittadini di Lottolandia hanno smesso di colpo di giocare al lotto, perché non sanno più cosa giocare.

Quando ci inganniamo da soli.

Chiacchiere di fisica di Stefano Marcellini
uando ci inganniamo da soli.
Quando stava per nascere mia figlia, al reparto maternità mi fu detta questa frase: “oggi è una giornata tranquilla, ma la settimana scorsa, che cambiava la Luna, non ci tenevamo dietro con le nascite”.
Io sapevo di questa storia della Luna che, con la fase giusta, favorirebbe il momento del parto. Non ci avevo mai creduto, perché dal punto di vista fisico non ha alcun senso, ma sul momento ho pensato che se lo dicevano al reparto maternità, qualcosa di vero doveva pur esserci. Anzi, chi meglio del personale del reparto maternità potrebbe sapere se la Luna con la fase giusta sia in grado di influenzare il momento del parto!
Uno può fermarsi a questa constatazione, che sembra molto ragionevole, e concludere che, visto che lo confermano perfino al reparto maternità, deve essere vero. Oppure si può fare qualcosa di più scientifico e oggettivo: uno studio statistico.
Si può quindi prendere un numero molto grande di persone scelte a caso, annotarsi le loro date di nascita, e dare il tutto in pasto a un computer, che mette in relazione quelle date di nascita con la fase lunare di quel giorno (ci sono software appositi), e produce un grafico del numero delle nascite in funzione del giorno del mese lunare, che dura circa 28 giorni. Se la fase lunare ha qualche effetto, ci si aspetterà di osservare una modulazione nel numero delle nascite durante il mese lunare. Se invece la Luna non ha effetto, si osserverà un grafico piatto, in cui il numero dei parti nei vari giorni lungo tutto il mese lunare è del tutto indifferente alla fase della Luna.
Questo studio è stato effettuato innumerevoli volte, in Italia e nel mondo, e il risultato è un grafico che, al netto delle fisiologiche fluttuazioni statistiche da giorno a giorno, più piatto non si può. Insomma: il presunto e declamato effetto della Luna nel favorire - a seconda della sua fase - il momento del parto, non esiste. È inventato. È una leggenda. Il fatto non sussiste.
Ma a questo punto ci si chiede come sia possibile che proprio al reparto maternità si siano sbagliati. Proprio quelli che vedono più nascite di chiunque altro! Proprio dove ingenuamente sarei andato a chiedere se è vera questa storia della Luna. Il motivo gli scienziati (e gli psicologi) lo sanno bene: si chiama “bias di conferma”.
Il bias di conferma funziona così: ognuno di noi, su qualunque argomento, scientifico, politico, sociale, ha dei pregiudizi, delle idee che, a torto o a ragione, ritiene corrette o sbagliate. E quindi, inconsciamente, si tende a valutare i fatti che si osservano attraverso la griglia di questi pregiudizi, dando un maggior peso a quei fatti che supportano le nostre convinzioni, e un peso minore a quelli che le negano. Il risultato è che, sempre inconsciamente, ci si convincerà di osservare nei fatti qualcosa che invece, alla luce di uno studio “unbiased”, cioè non influenzato da pregiudizi (nel caso della Luna basta una semplice statistica), non è mai avvenuto.
Quindi cosa sarà ragionevolmente successo al reparto maternità? Sarà successo che chi era già convinto dell’effetto della Luna sul momento del parto, il giorno in cui la Luna era quella giusta e c’erano effettivamente più nascite, avrà detto: “vedi? Per forza, c’è la Luna giusta!”. Il giorno in cui invece la Luna era quella giusta ma non c’erano più nascite del solito, non ci avrà fatto caso, o magari avrà pensato: “eh, vabbè, mica può essere sempre così tutte le volte! Però ti ricordi la volta scorsa?” Il risultato è che alla fine si sarà autoconvinto di avere realmente osservato nei fatti qualcosa che invece, proprio nei fatti, non è avvenuto.
Questa trappola del bias di conferma è molto subdola, e agisce sempre nel nostro modo di valutare ciò che accade attorno a noi. E agisce anche nella Scienza, e quindi anche nella fisica. E gli scienziati lo sanno bene, e cercano di cautelarsi in modo opportuno. Ad esempio, tutte le ricerche di nuovi fenomeni o di nuove particelle si fanno “in cieco”. Si decide a priori quella che dovrà essere la procedura di analisi, ottimizzandola in base a studi preliminari, ma senza analizzare i dati che riguardano esplicitamente lo studio che si vuole effettuare. Il rischio è altrimenti quello di manipolare più o meno inconsciamente la selezione dei dati stessi, ed estrarci quello che si sta cercando, convincendosi poi di averlo realmente osservato.
Perché non cadiamo nel pavimento?
Chiacchiere di fisica di Stefano Marcellini
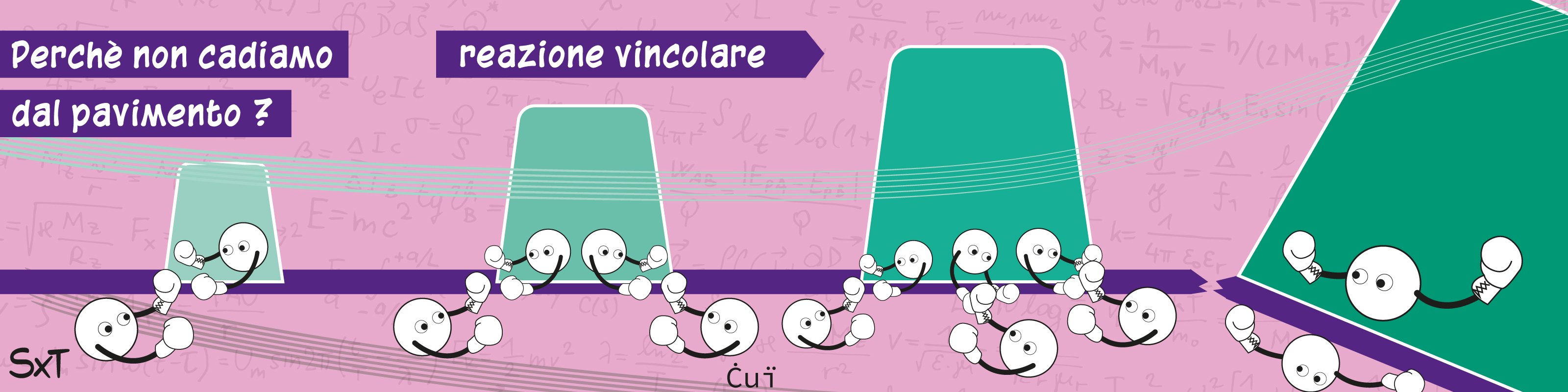
Una cosa che proprio non capivo al liceo era che se appoggiavi un corpo su un piano, il piano reagiva con la famosa "reazione vincolare", che era sempre uguale e opposta al peso del corpo. Come se il piano fosse intelligente. Ci metto un corpo da un chilo? Pronti con la reazione vincolare da un chilo! Ce lo metto da 10 chili? Ecco a voi una bella reazione vincolare da 10 chili giusti giusti! Il piano pensante! Io di sicuro non ero una cima, ma se semplicemente mi avessero fatto notare che mettendo un corpo da 10000 chili non avrei prodotto una reazione vincolare da 10000 chili ma avrei sfondato il pavimento, avrei capito. Sarebbe bastato così poco!
La reazione vincolare è il risultato della modifica della struttura della superficie del piano quando ci si appoggia sopra un peso. La struttura del piano di supporto si modifica (a livello microscopico se il peso è piccolo, e anche a livello macroscopico se non lo è) a causa del peso, e finché il corpo non sprofonda, per forza di cose la reazione vincolare è uguale e opposta al peso stesso, perché la somma delle forze deve essere zero. Se il corpo pesa poco, non c'è bisogno che il piano si scomodi troppo a modificarsi per bilanciarne il peso e non farsi trapassare. Se invece il corpo pesa molto, il piano deve adattarsi di brutto chiedendo ai legami delle molecole che lo compongono un grosso sforzo collaborativo. E se il corpo pesa troppo, le molecole dicono "basta, questo è troppo per noi" e il pavimento schiatta sotto il peso.
Ma la cosa interessante è l’origine della reazione vincolare. La forza che localmente sostiene il peso dell'oggetto è dovuta alla repulsione elettrica tra gli elettroni degli atomi del pavimento e quelli degli atomi dell'oggetto che ci appoggio sopra. La reazione vincolare è una forza elettrica! È infatti merito della presenza di cariche elettriche nella materia, che non serve solo a far accendere le lampadine, ma anche a non farci sprofondare nel pavimento!
Oltre alla repulsione elettrica fra elettroni c'è in realtà un altro fenomeno della natura che in qualche modo ci mette del suo: il Principio di esclusione di Pauli. Il principio di Pauli impedisce a particelle di spin semi-intero (1/2, per capirci) di stare nello stesso posto con la stessa energia e spin (con gli stessi "numeri quantici", per essere precisi). E gli elettroni, guarda caso, sono particelle di spin 1/2. Il risultato è che quando cerchiamo di avvicinare troppo gli elettroni degli atomi dell'oggetto che appoggiamo sul tavolo con gli elettroni degli atomi del piano di supporto, il Principio di Pauli entra in azione, e si manifesta tenendo lontano il peso quel tanto che basta a non essere violato. Questa stralunata legge che si studia in chimica al liceo ancor prima che in fisica, contribuisce a impedirci di sprofondare al piano di sotto. Ma fa anche altre incredibili magie, che magari racconteremo un’altra volta.
PS: esiste un certo dibattito su quanto sia effettivamente rilevante il Principio di Pauli nel non sprofondare nel pavimento. Alcuni dicono che il motivo sia sostanzialmente nella repulsione elettrica e basta. La mia opinione è che il Principio di Pauli sia comunque fondamentale, perché senza di esso gli atomi sarebbero radicalmente diversi, e sostanzialmente la materia non avrebbe il volume che ha. E la reazione vincolare, alla fine, è la materia che si ribella a chi vorrebbe ridurre il suo volume all'interno.

Incredibile scoperta fatta dai pesci

Chiacchiere di fisica di Stefano Marcellini
Incredibile scoperta fatta dai pesci
Sì, perché noi non lo sappiamo, ma anche tra i pesci ci sono gli scienziati, che dedicano la vita a studiare quello che per loro è l'Universo: il mare. Gli scienziati pesci, in questi ultimi anni, sono alle prese con un difficile problema: come è fatto l’Universo. In realtà da sempre i pesci si sono posti questo problema, prima ancora che anche tra di essi nascesse la Scienza. Ma oggi essi si chiedono come è fatto l’Universo non davanti alla propria tana, o nella propria zona di caccia, ma come è fatto su grande scala, su grandi distanze, in zone che mai saranno raggiungibili da nessun pesce, ma che con i mezzi della Scienza e della Ragione (che ai pesci non manca) sono comunque indagabili.
Al momento lo stato della conoscenza dei pesci sulla composizione dell’Universo è che esso è composto principalmente da sali. Ci sono sali di magnesio, di zolfo, di potassio, e anche vari carbonati, e poi nitrati, fosfati, e via via anche piccole percentuali di altri elementi. Tutto ciò i pesci lo chiamano genericamente Sale. Si può dire quindi in buona sostanza che l'Universo, per i pesci, è fatto di Sale.

Il bello della scienza
Chiacchiere di fisica di Stefano Marcellini
Molti pensano che la Scienza debba innanzitutto fornirci risposte. Risposte sulla struttura della materia, sul cosmo, sulla genetica, sulla biologia, sulla vita. Secondo tanti il progredire della Scienza sta nel ridurre il numero delle domande senza risposta sulla nostra comprensione della Natura. E spesso, quando gli scienziati raccontano dei mille problemi scientifici ancora aperti - la materia oscura, l’espansione accelerata dell’universo, i buchi neri, l’origine dell’universo stesso, la natura dei fenomeni quantistici, solo per citare problemi di fisica - un commento comune è “gli scienziati non ci capiscono niente”. L’innumerevole quantità di problemi senza risposta è vista da certi come l’incapacità della Scienza di comprendere i fenomeni che studia.
Sbagliato.

La cenerentola delle forze

Chiacchiere di fisica di Stefano Marcellini
La forza di gravità è stata storicamente la prima forza fondamentale ad essere osservata e studiata. Quando ancora non esistevano lampadine o computer capaci di mostrare esplicitamente l’esistenza delle forze elettriche, chiedersi cosa facesse sì che quando sfuggiva di mano qualcosa esso venisse sempre inesorabilmente attratto verso il basso, era una delle domande più fondamentali che ci si potesse porre. Newton mostrò che mele, Terra e pianeti, erano tutti vittime di ciò che chiamiamo forza di gravità.
Adesso sappiamo che esistono anche altre forze fondamentali, o interazioni, come le chiamano i fisici, oltre alla gravità. Esistono le interazioni elettromagnetiche, responsabili di tutti i fenomeni elettrici e magnetici e dell’esistenza e delle proprietà di ciò che genericamente chiamiamo luce. E poi esistono le interazioni nucleari forti e deboli, responsabili dell’esistenza e delle proprietà dei nuclei atomici e di fenomeni del mondo subnucleare, generalmente poco conosciuti al grande pubblico, ma che sono comunque di importanza fondamentale per garantire la nostra esistenza, tipo, ad esempio regolare i processi che avvengono all’interno del nostro Sole.
Ma esiste una gerarchia di intensità delle interazioni fondamentali? D’accordo, sono tutte importanti, e non potremmo fare a meno di nessuna di esse, ma qual è la più forte? E la più debole?

La forza di gravità sulla Luna

Chiacchiere di fisica di Stefano Marcellini
Tra i deliri del nuovo millennio c’è anche la credenza che non saremmo mai andati sulla Luna, e che le 6 missioni lunari, più quella fallita dell’Apollo 13 e le altre preparatorie, siano state tutte una messa in scena filmata in qualche hangar. Non intendo assolutamente mettermi a confutare gli argomenti dei No-Moon, ma essendo un fisico vorrei far notare un aspetto che in genere passa inosservato anche dagli stessi sostenitori del complotto: il campo gravitazionale sulla Luna, così come appare dai filmati degli astronauti.
Sulla superficie lunare il campo gravitazionale vale circa 1.6 m/s2, grosso modo il 17% che sulla superficie terrestre, dove è invece i famosi 9.8 dei problemi di fisica a scuola. Il valore è determinato dalla massa della Luna e dal suo raggio, entrambi diversi che per la Terra. Il risultato è che se sulla Terra peso 70 kg, sulla Luna ne peso 11. Ecco perché gli astronauti nei filmati saltellano sempre come Vispe Terese.

