Ho letto che con una funzione trascendente di Eulero si può estendere il calcolo del fattoriale ai numeri complessi: potreste spiegarmi come accade? (Alessandro Roncari) (2244_5291
Il fattoriale 
[45] di un numero naturale 
si definisce mediante le formule:
0! = 1, 1! = 1, e per n ≥ 2, n! = n · (n-1) · …1
oppure mediante definizione ricorsiva:
0! = 1, n! = n · (n-1)! per n ≥ 1 (1).
Eulero 
, cercando di interpolare n! per valore di n non intero , cioè di definire il fattoriale di un qualsiasi numero reale positivo, introdusse la funzione:
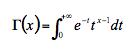detta funzione gamma.
Si può dimostrare facilmente che Γ(n + 1) = n! per ogni numero naturale n.
Per questo la si definisce:
(2)
Si dimostra che 0!=1 e x! = x • (x –1)! , quindi la (2) può venire considerata una estensione della (1). Per esempio, sapendo che dal calcolo diretto risulta:
si può ottenere:
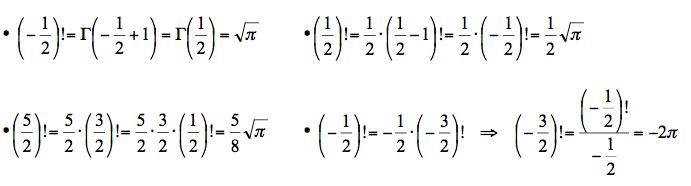
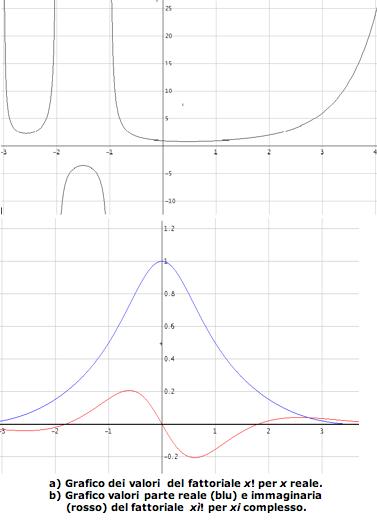
La formula (2) si può estendere ai numeri complessi ix. Anche in campo complesso valgono le formule 0!=1 e x! = x • (x –1)!
Irene Guagnini – Docente di matematica