|
|
Vorrei avere una spiegazione semplice su cosa si intende per tunnel quantistico (Anonimo) |
consecutive, una più bassa dell'altra, separate da una valle, su cui si muove senza attrito una pallina di massa m, soggetta a un campo gravitazionale uniforme, come quello esistente alla superficie della terra. Il profilo ha il solo scopo di obbligare la pallina a muoversi lungo di esso, senza compiere lavoro (in queste condizioni la forza generata dal vincolo (reazione vincolare) è sempre ortogonale alla direzione della velocità, così da non compiere lavoro). È abbastanza intuitivo prevedere che, se si abbandona la pallina in quiete nel punto A (sommità della collina di sinistra) in modo che essa scivoli verso la valle, questa acquisterà velocità man mano che discende, fino a raggiungere la velocità massima al fondo della valle, dopo di che essa risalirà la china del versante opposto della seconda collina, fino a fermarsi in quiete nel punto B, alla stessa altezza del punto A, per poi ridiscendere e fermarsi successivamente al punto A. La meccanica classica spiega questo comportamento dicendo che nel primo tratto (dal punto A al fondovalle) . l'energia cinetica aumenta a spese dell'energia potenziale del campo gravitazionale e nel secondo tratto (dal fondovalle al punto B) l'energia cinetica diminuisce nel contempo che cresce quella potenziale, in modo tale che la somma delle due forme di energia sia sempre costante. Si può dimostrare che l'energia potenziale del campo gravitazionale varia come mgh, dove m è la massa della pallina, g l'accelerazione di gravità alla superficie della terra e h la variazione di quota della pallina stessa. In queste condizioni la pallina non supererà mai la sommità della collina di destra, perchè non avrà mai abbastanza energia cinetica per farlo. Questa è la conclusione della meccanica classica. Dal punto di vista della meccanica quantistica le cose vanno diversamente. Nella descrizione quantistica si associa alla particella materiale un'onda la cui intensità in un particolare punto dello spazio fornisce la probabilità di trovarla in quel punto in una serie ripetuta di prove dello stesso esperimento. L'equazione che governa l'evoluzione di questa onda di probabilità è nota come Equazione di Schrodinger. Se si pone la pallina nella valle tra le due colline con una energia totale tale che dal punto di vista della meccanica classica essa vi rimane intrappolata, si trova invece una probabilità non nulla di trovarla all'esterno delle due colline; è come se la pallina riuscisse a scavarsi un tunnel sotto una delle due colline per uscire dalla valle, di qui il nome di effetto tunnel! Nel caso esaminato di oggetti con masse e dimensioni macroscopiche questa probabilità è infinitamente piccola, così che le predizioni della meccanica quantistica coincidono sostanzialmente con quelle della meccanica classica, in accordo con l'esperienza (il tempo necessario per eseguire una serie ripetuta di esperimenti in modo da vedere almeno una volta la pallina al di là della barriera costituita dalle due colline supera di moltissimi ordini di grandezza la vita stessa dell'universo!). Tuttavia la differenza concettuale è notevole,perchè la probabilità non è rigorosamente zero.
Calogero Natoli – Fisico |
||
|
|
||
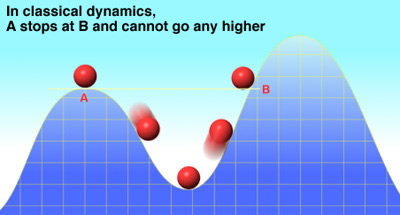fig. 1
Le differenze predittive tra le due meccaniche si fanno vistose se dal mondo macroscopico si passa a quello microscopico, con masse e dimensioni dell'ordine di quelle atomiche ( 10-24~10-27 g e 10-8~10-13 cm ). E' il caso ad esempio dei nuclei di particelle Alpha, costituiti da due protoni e due neutroni, contenuti all'interno di un nucleo di massa atomica A e numero atomico Z (Z rappresenta il numero di protoni nel nucleo e A-Z il numero di neutroni). Se Z = 92 e A = 238, si tratta di un isotopo dell'Uranio. Sperimentalmente si osserva che molti nuclei con numero di massa A > 210 emettono spontaneamente particelle Alpha con energie cinetiche, misurate a grande distanza dal nucleo, comprese tra i 4 e 9 Milioni di elettroni-Volt (MeV), quindi di molto inferiore a quella necessaria per superare le forze di attrazione nucleare esercitata su di esse da parte del resto del nucleo che si calcola (e si misura!) essere dell'ordine di 25 MeV. Per la meccanica classica il processo non dovrebbe avvenire! Il fenomeno è quindi inspiegabile secondo lo schema classico e la sua spiegazione costituì uno dei primi trionfi della meccanica quantistica, quando nel 1928 fu avanzata da Gamow 