0095. Quante geodetiche passano per due punti di un cono?

 Quante geodetiche passano per due punti di un cono? (Mariangela Rossi)

 La geodetica è una curva con lunghezza estrema (minima o massima); nello spazio la geodetica ha la lunghezza minima rispetto a tutte le curve prossime che uniscono due punti A e B. La geodetica tra i punti A e B è proprio il segmento AB, che ha la minore lunghezza rispetto alle altre linee tra A e B. Sulla sfera la geodetica fra due punti A e B è ciascuno dei due archi con estremi in A e B appartenenti a una circonferenza massima della superficie. In modo intuitivo una geodetica si ottiene camminando sulla superficie senza deviazioni laterali.

La determinazione delle geodetiche è un problema arduo di un capitolo della matematica denominato calcolo delle variazioni. In geometria analitica il cono va inteso con generatrice infinita (fig.1).

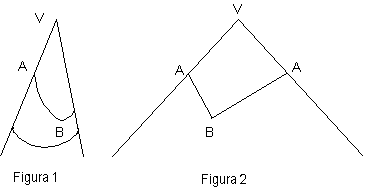
Su questa superficie si dovrebbe applicare la suddetta teoria per ottenere la forma delle geodetiche. Però, la possibilità di sviluppare la superficie conica in un angolo piano (fig.2), consente di risolvere il quesito posto con semplicità. Stabiliti i due punti diversi A e B sul cono, eseguiamo lo sviluppo a partire dalla generatrice passante per A. In tal modo A si scinde in due punti, da cui si possono tracciare due segmenti AB, che sono geodetiche perché la loro lunghezza è minima rispetto a quella delle curve attigue. A questo punto basta tramutare l’angolo nel cono originario per trasformare i due segmenti nelle corrispondenti geodetiche. Quindi, fra due punti del cono si possono tracciare due geodetiche, che coincidono se un punto diventa il vertice del cono. Tuttavia esistono altre geodetiche che si possono disegnare girando più volte intorno al cono. Riportando sul piano in senso antiorario gli sviluppi successivi del cono di ampiezza q, si ottengono n segmenti BA che producono altrettante geodetiche (fig. 3).

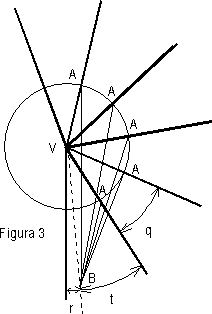Poiché nq-r ≤ 180° si deduce che n=parte intera di 

\[\frac{180^\circ +r}{q}\]

Un discorso identico si può ripetere per le geodetiche che si avvolgono in senso orario in numero m=parte intera di

\[\frac{180^\circ +t}{q}\]

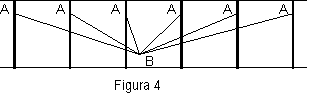
Le geodetiche che si possono tracciare per due punti differenti di un cono sono allora m+n; se le due quantità in parentesi sono contemporaneamente intere, due di queste linee passano per il vertice e si sovrappongono; quando A si porta in V, tutte le geodetiche si trasformano nel segmento BV. Nell’esempio di q = 70°, r = 50°, t = q-p = 20°, si hanno 5 geodetiche. In particolare, per un cono che degenera in un piano si ha q = 360° ed m+n=1, in conformità al numero di geodetiche conducibili per due punti distinti di un piano. Quando l’apertura del cono diminuisce, m+n tende a crescere. Nel cilindro il numero di geodetiche è infinito come evidenziato in alcuni suoi sviluppi consecutivi orari ed antiorari riportati in fig.4.

Il problema della ricerca degli estremi si presenta anche quando la luce si riflette su una superficie speculare. In base al principio di Fermat , la radiazione segue il percorso che richiede il tempo minimo. Da ciò si possono derivare facilmente le leggi della riflessione. Una questione risolvibile col calcolo delle variazioni consiste nel determinare la traiettoria che deve descrivere un corpo, fra due punti in un piano verticale senza attrito, nel tempo minimo. Si deduce che la curva ha la forma di una cicloide. Infine, nella relatività generale le particelle in volo libero seguono tragitti geodetici nello spazio-tempo.

Pasquale Catone – Docente di Fisica