|
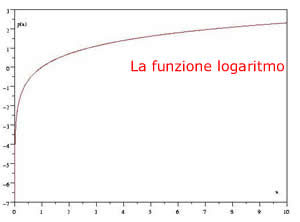
Approfondimento a cura della redazione di ScienzaPerTutti fig. 1 La funzione logaritmo, tracciata in figura 1, è una funzione sempre crescente, negativa per valori di x compresi tra 0 ed 1 e positiva per x>1. I l logaritmo è definito solo per valori positivi di x. Diciamo che una variabile aleatoria Y è lognormale se la distribuzione di probabilità del logaritmo di Y è una gaussiana.Se Y è una variabile aleatoria lognormale, allora la sua distribuzione di probabilità avrà un aspetto come in figura 2.
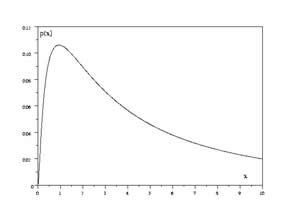
fig. 2 una distribuzione di probabilità lognormale Si noti, confrontando la figura 2 con il grafico riportato nella scheda di approfondimento sulle variabili gaussiane, che una distribuzione lognormale non ha una forma “a campana” simmetrica rispetto al suo massimo. Si noti inoltre che questa distribuzione è definita solo per gli x positivi: una variabile lognormale non sarà mai negativa. |