di F. L. Fabbri, L. Benussi, E. Durante, S. Bertolucci , G. Isidori
Mr. Quadro non può vedere Madame Sfera nella sua interezza, ma non vede neppure il profilo della sezione, in quanto non lo può vedere dall'alto; vede quindi solo una linea che aumenta di lunghezza e poi diminuisce sino a sparire, un fatto che non può spiegare.
|
Fonte illustrazione:
http://www.treccani.it/site/scienze6.htm
|
Questo curioso esempio ci dice, in modo rudimentale ma efficace, come alcuni fenomeni o leggi della fisica difficili da comprendere nelle tre dimensioni potrebbero invece trovare una spiegazione più semplice e risultare addirittura banali se li immaginassimo accadere in quattro o più dimensioni. Visualizzare uno spazio a quattro o più dimensioni per noi non è facile, ma ci viene in aiuto la matematica: da molto tempo infatti i matematici sanno come trattare le extradimensioni.
|
Bernhard Riemann 
, in un famoso seminario tenutosi il 10 giugno 1854 all'Università di Göttingen (in Germania), introdusse per la prima volta una teoria sullo spazio con più di tre dimensioni. Nel 1919 un altro matematico, il polacco Theodor Kaluza , suggerì che l’Universo in cui viviamo avesse effettivamente quattro dimensioni spaziali. In questo spazio a quattro dimensioni le leggi dell’elettromagnetismo di Maxwell e della gravità di Einstein , che ci appaiono così diverse nelle nostre tre dimensioni, discenderebbero le une dalle altre. Il gravitone - il quanto del campo gravitazionale 
- e il fotone - il quanto del campo elettromagnetico - così diversi per i nostri esperimenti tridimensionali, diventano parenti strettissimi nello spazio quadridimensionale di Kaluza. Ma se l'Universo ha veramente più di tre dimensioni perché noi non riusciamo a visualizzarle?
L'idea implicita nel lavoro di Kaluza, sviluppata in maniera più completa nel 1926 dal matematico svedese Oskar Klein , è che l'Universo abbia dimensioni estese e dimensioni curve raggomitolate su se stesse. Cosa vuol dire?
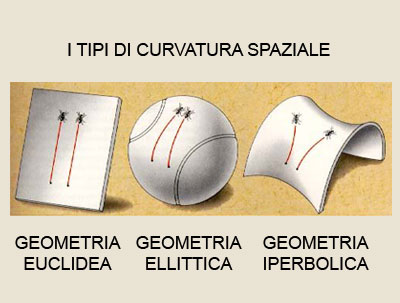
Per capirlo dobbiamo, per prima cosa, introdurre il concetto di curvatura spaziale e per farlo torniamo a Flatlandia. Lo spazio a due dimensioni può essere senza curvature, come un foglio di carta piano, ovvero può essere curvato nella terza dimensione. Basta pensare ad un telo elastico sul quale disponiamo un oggetto pesante. La superficie si curverà attorno al peso e due rette, tracciate parallele sul telo, tenderanno ad avvicinarsi. La geometria Euclidea, gioia e tormento di tutti gli studenti, si applica agli spazi piani. Furono i matematici Nikolaj Ivanovic Lobacevskij 
e Yános Bolyai ;negli anni tra il 1830 e 1850 - a discutere i primi esempi di geometrie non-euclidee in cui non è valido il famoso V postulato di Euclide sulle rette parallele.ùCome altri esempi di uno spazio “curvo”, si pensi alla superficie di una sella o di una sfera.