0244. Perché l'orbita della Terra intorno al Sole è ellittica?

Perché l'orbita della Terra intorno al Sole è ellittica (anche se di poco)?.Ci sono è vero le leggi di Keplero e di Newton ma, più che altro, queste leggi sembrano dei dati presi dall'osservazione che non mi fanno capire il perché delle cose. Newton ci dice che (per esempio) quando la Terra si allontana dal Sole, la sua velocità diminuisce, ma come succede che la Terra si allontana dal Sole? Se chiedessi perché la Terra si allontana dal Sole mi si risponderebbe che ciò avviene, perché la sua velocità diminuisce, (il gatto che si morde la coda) La Terra quando si trova nel periodo dell'anno in cui è più vicina al Sole mantiene dall'astro una certa distanza, ed è soggetta all'attrazione gravitazionale per un certo valore a cui per esempio potrei dare il valore 100. Poi succede che pur rimanendo questo valore sempre uguale e cioè 100, la Terra comincia pian piano ad allontanarsi e a diminuire di velocità. Cosa interviene a rallentare il moto della Terra? O chi interviene a deviare la Terra dal suo percorso che sarebbe molto più facilmente comprensibile se fosse un moto circolare e non una ellisse.

(Luca)

Dobbiamo partire dal fatto che esiste la forza di gravità o forza di gravitazione universale. Sai già che la forza gravitazionale che si esercita tra due corpi di massa M₁ e M₂ che si trovino a distanza R uno dall’altro è uguale a:

\[F=\frac{G\cdot M_1 \cdot M_2}{R^2}\]

La forza F si misura in Newton (se applichi ad un oggetto di 1 Kg una spinta che fa aumentare la sua velocità di 1 metro al secondo per ogni secondo che passa, quella spinta è di 1 Newton) G è la costante di gravitazione universale [49] e il suo valore è: 6.67 x 10 ^–11 se le masse sono espresse in kg e le distanze in metri. La forza è diretta lungo la congiungente le due masse ed è ovviamente attrattiva.

Consideriamo il moto di un pianeta che orbita attorno al Sole, per esempio la Terra: la forza che agisce sulla Terra è sempre e costantemente diretta verso il Sole ed è l'unica forza presente (trascurando altre forze di minore intensità come quelle della Luna e di altri pianeti). Si può dimostrare matematicamente che date queste condizioni (intensità della forza di gravitazione e direzione della forza) le orbite stabili sono necessariamente delle ellissi il cui schiacciamento è determinato dalle condizioni iniziali di inserimento nell'orbita.

Perché le orbite non sono circolari?

Semplicemente perché un cerchio è solo un caso particolare di ellisse [49] . Certo potrebbe anche capitare che un pianeta percorra un'orbita circolare per puro caso ma è molto più probabile che durante le fasi della formazione del sistema solare, il pianeta si sia stabilizzato su un'orbita ellittica, magari poco ellittica, ma comunque non perfettamente circolare. Considerando il caso di un’orbita perfettamente circolare (anche se improbabile nella realtà), essendo la forza diretta lungo la congiungente i due corpi, vediamo che istante per istante questa forza è perpendicolare alla traiettoria del pianeta e quindi alla velocità che rimane costante come valore, anche se cambia direzione, perché la velocità è diretta sempre tangente all’orbita. In questo caso avremo un moto circolare uniforme. Non bisogna lasciarsi confondere dalla parola "uniforme": infatti, uniforme è il valore numerico della velocità, poniamo 30 km/s, che rimane costante, ma la velocità in realtà varia perché istante per istante cambia la sua direzione. Questo accade perché c'è la forza gravitazionale. Se il pianeta non fosse assoggettato a questa forza, allora sì che il suo moto sarebbe veramente uniforme: la sua velocità non solo non cambierebbe di valore ma neanche cambierebbe la sua direzione che rimarrebbe costante (moto rettilineo uniforme).

Nel caso di una orbita ellittica avremo che, essendo la forza sempre diretta lungo la congiungente, in alcune parti dell’orbita la forza contribuirà a “frenare “ il pianeta quindi a rallentarlo: ciò accadrà nei punti in cui la velocità e la forza formano un angolo maggiore di 90 gradi. In altri punti la forza tenderà ad accelerare il pianeta: ciò accadrà nei punti dove la forza e la velocità formano un angolo minore di 90 gradi (ora mi sto riferendo al valore numerico della velocità). Se il nostro web-nauta prova a disegnare un ellisse con il Sole in uno dei fuochi e il pianeta può visualizzare facilmente quanto ho detto.

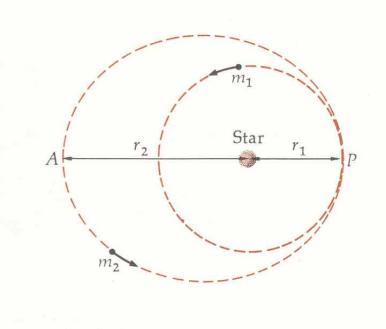Alla fine della sua mail il nostro web-nauta Luca scrive : "…..La Terra quando si trova nel periodo dell'anno in cui è più vicina al Sole mantiene dall'astro una certa distanza, ed è soggetta all'attrazione gravitazionale per un certo valore a cui per esempio potrei dare il valore 100. Poi succede che pur rimanendo questo valore sempre uguale e cioè 100, la Terra comincia pian piano ad allontanarsi e a diminuire di velocità. Cosa interviene a rallentare il moto della Terra? O chi interviene a deviare la Terra dal suo percorso che sarebbe molto più facilmente comprensibile se fosse un moto circolare e non una ellisse……" Il valore della velocità della Terra nel punto che viene considerato dipende non solo dalla distanza ma dall'orbita nel suo insieme. La figura rappresenta le orbite di due differenti pianeti: uno con orbita perfettamente circolare l'altro con orbita ellittica, entrambi hanno nel punto P la stessa distanza dalla stella centrale. Il pianeta m₁ e il pianeta m₂ nel punto P sono soggetti alla stessa forza gravitazionale (ce lo dice la legge di cui sopra) ma m₂ arriverà nel punto P con una velocità maggiore di quella di m₁, perché viene "da più lontano" e sebbene quando era distante la forza era piccola, questa forza formava con la velocità un angolo minore di 90 gradi quindi faceva acquistare velocità al pianeta. Quando m₂ arriva nel punto P la sua velocità è troppo alta per inserirsi sull'orbita circolare e quindi si allontanerà pian piano dalla stella e di nuovo comincerà a rallentare fino al punto A quando invece ricomincerà a riacquistare velocità.

Sandro Barbanera - Fisico