|
|
Esiste una formula che permetta di calcolare il numero di diagonali di un solido? (Elia) (2219_3200_5555) |
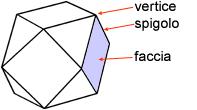
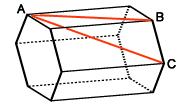
-quante diagonali ha un poligono ? Il numero d di diagonali di un poligono di Jordan -quante diagonali ha un poliedro? Il numero d di diagonali di un poliedro di Eulero I termini poligono di Jordan e poliedro euleriano indicano quello che comunemente s'intende per "poligono" e "poliedro". In breve ecco le definizioni sintetiche: - Poligonale (di Jordan) = linea spezzata chiusa piana che non si interseca e che divide il piano in due regioni chiamate interna ed esterna. In termini più tecnici una poligonale è un caso particolare di curva di Jordan. - Poligono = figura piana formata da una poligonale e dalla parte di piano interna ad essa. Diagonale di un poligono = segmento che congiunge due vertici non appartenenti ad uno stesso lato. - Poliedro euleriano = solido senza "buchi passanti" limitato da facce che sono poligoni. Poliedro per cui vale la formula di Eulero - Diagonale di un poliedro = segmento che congiunge due vertici non appartenenti ad uno stesso spigolo. Vediamo ora di dimostrare le formula che abbiamo brevemente menzionato. Il linguaggio dei poliedri Le due figure seguenti illustrano i principali elementi dei poliedri: vertice, spigolo, faccia, diagonale.
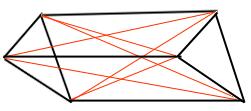
Il numero delle diagonali di un poligono. Cominciamo dal caso più semplice quellodel poligono. Immaginate v punti nel piano, i vertici di un poligono di v lati. Se colleghiamo ciascun vertice con tutti gli altri, quanti segmenti distinti possiamo individuare? Poichè ciascuno dei v punti si può collegare con altri (v-1) punti, la risposta sembrerebbe – molto semplicemente essere v(v-1). Ma non è così. In realtà bisogna dividere il risultato per 2 perché ogni collegamento in questo modo vienecontato 2 volte. Ad esempio, per due punti A, B, è stato contato sia il collegamento AB che il collegamento BA. Dunque, v punti nel piano individuano v(v-1)/2 segmenti che li congiungono. Ma se vogliamo calcolare quante sono le diagonali dobbiamo sottrarre il numero dei lati, che è v. Ecco dunque la formula che avevamo anticipato: d = v (v-1) /2 - v = v(v-3)/2. Il numero delle diagonali di un poliedro. Passiamo ora dal piano allo spazio tridimensionale. Immaginate v punti nello spazio, vertici di un poliedro. Come nel caso precedente, essi determinano v (v-1)/2 segmenti. Se vogliamo calcolare quante sono le diagonali del poliedro, dobbiamo sottrarre il numero degli spigoli, e qui viene il difficile! Infatti conoscendo soltanto il numero dei vertici di un poliedro, non possiamo sapere quanti sono gli spigoli, e neppure quante sono le facce quante. Ad esempio, un prisma triangolare e un ottaedro hanno entrambi 6 vertici, ma:
In ognuno dei due casi, comunque, vale la formula di Eulero : F - S + V = 2 . Quindi, per calcolare il numero di diagonali, d, di un poliedro occorre conoscere anche il numero degli spigoli, s, oltre a quello dei vertici, v, e la formula allora sarà: d = v (v-1) /2 - s. Applichiamo la formula trovata ad alcuni poliedri. Prisma triangolare: v=6, s=9 Il numero di diagonali è: d = (6 x 5 : 2) - 9 = 6
Figura3. Prisma triangolare v=6, s=9 Ottaedro: v=6, s=12 Il numero di diagonali è : d = 6 x 5 : 2 - 12 = 3
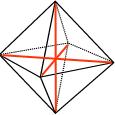
Figura 4.Ottaedro v=6, s=12 Tetraedro: v=4, s=6 Il numero di diagonali è :
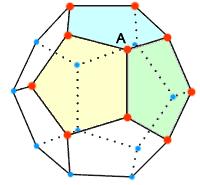
Figura 5. Tetraedo v=4, s=6. Il tetraedro è un poliedro senza diagonali! Dodecaedro: v=20, s=30 Il numero di diagonali è : d = 20 x 19 : 2 - 30 = 160
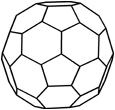
Figura 6. Dodecaedro v=20, s=30 Per calcolare il numero di diagonali del dodecaedro useremo un'altra tecnica che, comunque, vale anche per tutti gli altri poliedri. Da ogni vertice, ad esempio A, escono 10 diagonali interne al poliedro. Poiché i vertici sono 20, in tutto abbiamo 20 x 10 : 2 = 100 diagonali interne. Inoltre su ogni faccia pentagonale si trovano 5 x 3 : 2 = 5 diagonali. In tutto abbiamo 5 x 12 = 60 diagonali nelle facce. Complessivamente le diagonali del dodecaedro sono quindi 100 + 60 = 160. Icosaedro troncato: (il pallone da calcio) v=60, s=90 Il numero di diagonali è : d = 60 x 59 : 2 - 90 = 1680
Figura 7. Icosaedro troncato v=60, s=90 Proponiamo ora ai nostri web-nauti due esercizi abbastanza semplici: Quante diagonali ha una piramide a base quadrangolare?
Figura 8. Piramide a base quadrangolare Quante diagonali ha un cubo?
Figura 9. Cubo Ancora un esempio con un poliedro concavo
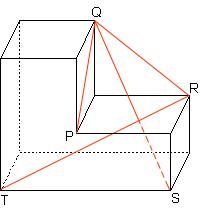
Figura 10. Un poliedro concavo a forma di “L” v=12,s=18. Questo polietro a L ha 48 diagonali Nel "poliedro a L"si notano: QR, una diagonale completamente esterna; QS, una diagonale che giace in parte all'esterno e in parte all'interno del poliedro; QP, una diagonale che giace su una faccia; RT, una diagonale interna al poliedro. Diagonali interne : un problema da esaminare caso per caso. Sia i poligoni sia i poliedri possono avere: diagonali completamente interne diagonali parzialmente interne diagonali esterne (tranne gli estremi) Non esiste una formula generale per calcolare il numero di diagonali interne. Bisogna esaminare le figure caso per caso. Nel caso dei poliedri convessi, tuttavia, si può applicare un semplice algoritmo: diagonali interne = diagonali - somma delle diagonali di tutte le facce. Un esempio: le diagonali interne dell'ottaedro troncato v=24, s=36, f=14, di cui 6 quadrati e 8 esagoni.
Figura 11. Ottaedro troncato Diagonali del poliedro: d = 24 x 23 : 2 - 36 = 240 Diagonali dei quadrati: 2 x 6 = 12 Diagonali degli esagoni: 9 x 8 = 72 Diagonali interne del poliedro = 240 - (12 + 72) = 156 Gianfranco Bo – Matematico |
||||
|
|
||||