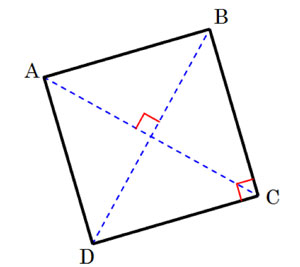
Quadrato E' un parallelogramma con tutti i quattro gli angoli eguali tra loro ( 90°) . I quattro lati sono di eguale lunghezza.
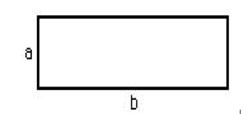
Rettangolo E’ un parallelogramma con i tutti i quattro angoli uguali tra loro (90°) e i lati uguali a due a due (lati opposti)
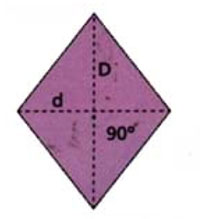
Rombo E’ un parallelogramma con gli angoli uguali a due a due (gli opposti): due acuti (maggiori di 90°) e due ottusi (minori di 90°) . I quattro lati sono uguali.
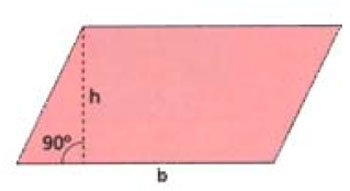
Parallelogramma generico: i suoi lati opposti sono paralleli, gli angoli uguali a due a due come nel rombo, ma diversamente dal rombo i lati non sono - necessariamente - tutti eguali, ma eguali a due a due ( gli opposti). Nel quadrato, nel rettangolo ed anche nel rombo le due diagonali sono tra loro uguali. In un parallelogramma generico, che non coincida con i casi precedenti, le due diagonali si intersecano a metà ma non sono tra loro uguali. Come si calcola allora la lunghezza della diagonale maggiore ? Se si conoscono le lunghezze dei lati e gli angoli del quadrilatero si costruisce un triangolo che ha lati la diagonale da calcolare, e gli altri due i lati del quadrilatero. La diagonale in seguito si calcola applicando il cosiddetto "teorema del coseno" Il teorema del coseno : Se a, b, c sono i lati di un triangolo e α è l’angolo compreso tra i lati b e c vale la relazione : \[a^2 = b^2 + c^2 - 2bc~ cos(\alpha)\] Il teorema è una generalizzazione di quello di Pitagora al quale si riduce quando α=90° (cos90=0). Lazare Carnot lo riporta in un suo libro nel 1800, tuttavia il teorema era già noto ad Euclide Catalina Curceanu (Petrascu) – Fisico |
0379. Come si calcola la diagonale maggiore di un parallelogramma?
Come si calcola la diagonale maggiore di un parallelogramma? (Luca Abate)