0067. Come si calcola la velocità angolare di un cilindro sottoposto a forza tangenziale costante?

 Supponiamo di avere un cilindro di massa M libero di ruotare sul suo asse longitudinale e che gli venga impressa una forza tangenziale costante di intensità F. Come si determina, consideranto trascurabili gli attriti, la velocità angolare raggiunta dal cilindro? (Emanuele Guidoni)

In base al secondo principio della dinamica, una massa è uguale al rapporto tra la forza a cui è sottoposta e l’accelerazione che acquista; quindi, la massa indica un’inerzia alle accelerazioni. Il momento d’inerzia rispetto ad un asse s, attorno a cui ruota un corpo, è uguale al rapporto tra il momento delle forze relativo a s e l’accelerazione angolare acquisita; dunque, il momento d’inerzia del corpo rappresenta una resistenza alle accelerazioni angolari. Il momento d’inerzia si può determinare direttamente sommando i prodotti delle singole masse infinitesime costituenti il corpo per i quadrati delle loro distanze dall’asse. Ne segue che allontanando le masse dall’asse, cresce il momento d’inerzia. Allora è più facile produrre accelerazioni angolari disponendo le stesse masse vicino all’asse che lontano.

Poiché il momento d’inerzia I del cilindro omogeneo di densità r, raggio R e massa M, rispetto al suo asse longitudinale s, è I =MR²/2 e il momento della forza relativo ad s è t = FR, l’accelerazione angolare del corpo a = t/ I = 2F/ (MR) risulta proporzionale alla sollecitazione F e inversamente proporzionale alla massa e al raggio del cilindro. Per F, M, R assegnati, il cilindro è in rotazione uniformemente varia in quanto l’accelerazione angolare è costante. Dalla definizione dell’accelerazione angolare, si ricava la velocità angolare w al tempo t con la seguente formula: w= w₀ + at = w₀ + 2Ft / (MR), essendo w₀ la velocità angolare al tempo zero. La w ha un andamento lineare col tempo; in particolare w= 2Ft / (MR) è proporzionale al tempo, se il cilindro si trova inizialmente in quiete.

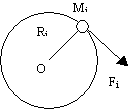
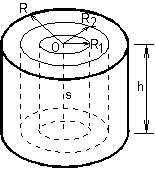
Come spiegare l’equazione t = Ia della dinamica rotazionale?

Sia  M_i una massa puntiforme vincolata a muoversi su una circonferenza di centro O e raggio R_i e soggetta alla reazione vincolare radiale verso O e alla forza F_i tangente alla traiettoria. Oltre all’accelerazione centripeta verso O, la massa acquista anche un’accelerazione ai parallela e concorde alla forza F_i = M_ia_i, in virtù del secondo principio della dinamica. La rapidità di variazione nel tempo della velocità del corpo v_i = wR_i, fornisce la relazione per l’accelerazione tangenziale a_i = aR_i. Dato che Fi = M_iaR_i si ha F_iR_i = M_iaR_i² ovvero t_i = I_ia, dove t_i è il momento della forza ed I_i = M_iaR_i² il momento d’inerzia della massa rispetto a O.

Per un corpo rigido rotante attorno ad un asse s, si perviene a t = Ia sommando tutti i contributi t_i = I_ia , dove t = ? t_i e I =? M_iaR_i² . In t rientra soltanto il momento delle forze esterne rispetto ad s perché l’azione e la reazione, essendo opposte e giacenti sulla stessa retta per il terzo principio della dinamica, producono un momento nullo. La R_i nell’espressione del momento d’inerzia I del solido, è la distanza della massa M_i dall’asse s.

Perché il momento d’inerzia del cilindro vale I = MR²/2?

Per dimostrare la formula si potrebbe applicare il metodo dell’integrazione. Qui viene proposto un facile procedimento alternativo. La massa del corpo di raggio R vale: M=R²hpr = kR², dove k = hpr; quindi i momenti d’inerzia dei cilindri di raggio R₂ ed R₁ con masse M₂ ed M₁ sono I₂ = kR₂⁴/2 ed I₁ = kR₁⁴/2. Il momento d’inerzia dello strato cilindrico con raggi R₁ e R₂ e massa DM, è DI = I₂-I₁= k(R₂⁴-R₁⁴)/2 = k(R₂²-R₁²) (R₂²+R₁²)/2 = (M₂-M₁) (R₂²+R₁²)/2= DM R_m², in cui R_m² è la media dei quadrati dei due raggi R₁ ed R₂. Se lo strato è molto sottile, R₁ tende a R₂ ed il momento d’inerzia tende alla massa per il quadrato del raggio. Ma questo risultato coincide proprio con la definizione del momento d’inerzia dello strato. Pertanto I=MR²/2 è l’espressione esatta del momento d’inerzia del cilindro. Si può obiettare che la spiegazione funziona pure per I=MR²/2 + costante; però I si deve annullare per R=0 e ciò implica l’azzeramento della costante. La crescita lineare col tempo della velocità angolare, trovata in precedenza, dovrebbe portare la w a valori sempre più elevati. Ma la velocità periferica del cilindro non può superare la velocità della luce. A velocità prossime a quella della radiazione luminosa nel vuoto, il problema si dovrebbe trattare con la relatività. In tali condizioni, tuttavia, le forze centripete diventano enormi ed il corpo finirà per perdere la sua rigidità.

Pasquale Catone - Docente di fisica