Approfondimento a cura di Speranza Falciano
Un numero complesso è per definizione una coppia ordinata di numeri reali (a,b) che può essere rappresentata algebricamente come a+ib dove a è la parte reale e ib la parte immaginaria, tenendo conto che i2 = -1 (per convenzione si usa la lettera i per immaginario). E’ inoltre possibile e utile rappresentare geometricamente i numeri complessi introducendo una corrispondenza biunivoca tra essi e i punti di un piano (piano complesso) con coordinate cartesiane ortogonali a e b.
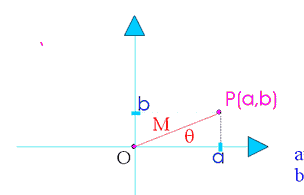immagine estratta dal sito www.electroportal.net
In tal modo ai numeri reali (a) vengono a corrispondere i punti dell’asse x (asse reale) e ai numeri immaginari puri (ib) i punti dell’asse y (asse immaginario). Il piano complesso viene anche detto piano di Gauss 
- In questo modo si possono individuare i numeri complessi attraverso vettori del piano aventi modulo sqrt(a2+b2) e applicati all’origine. I numeri complessi furono introdotti dagli algebristi italiani nel ‘500.