di Patrizia De Simone
Coniugazione di Carica e Inversione Spaziale
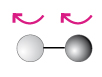
Proviamo ora ad applicare la coniugazione di carica (C) e successivamente un’inversione spaziale (P) ad un sistema di due sfere, una bianca ed una nera, che ruotano in senso orario. Cosa succede? Otteniamo un sistema di due sfere, una bianca ed una nera, che ruotano in senso... anti-orario. Cioè, il sistema non è invariante rispetto ad una operazione combinata di C e P (vedi figura sotto).

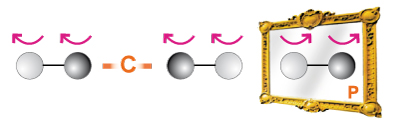
Coniugazione di Carica e Inversione Spaziale e Inversione Temporale
Per ottenere nuovamente il sistema iniziale, cioé due sfere bianca e nera che ruotano in senso orario, bisogna applicare anche un'operazione di inversione temporale T!!(vedi figura)
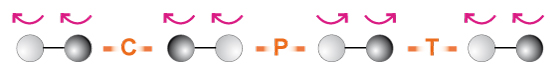
Ebbene, i fisici hanno introdotto queste simmetrie per tentare di semplificare la descrizione del mondo sub-nucleare e con la non celata speranza di scoprire che le interazioni tra le particelle fossero invarianti separatamente per inversione spaziale P, inversione temporale T e coniugazione di carica C. In realtà la natura non è cosi semplice ... ad esempio le interazioni deboli non sono invarianti per riflessione spaziale né per coniugazione di carica e nemmeno per l'operazione combinata di P e C ...!!! Per quanto sappiamo ora, il mondo sub-nucleare è invariante solamente rispetto all’operazione combinata di C, P e T, ovvero la simmetria CPT.

