Un altro duro colpo al determinismo classico venne sferrato da Werner Heisenberg con il suo principio di indeterminazione che mina alle fondamenta l'idea che, conoscendo ad un dato istante la posizione e la velocità di una particella, si riesca a conoscerne il valore ad un qualunque tempo successivo (nel paragrafo precedente, abbiamo definito questa situazione con il termine di determinismo). La relazione di indeterminazione riguarda per l'appunto la precisione Δ con cui possiamo conoscere posizione e velocità di una particella e recita cosi:
Δx Δ(mv) >= h /4 π
(1)
e significa che tanto meglio si conosce, ad esempio, la posizione, tanto peggio possiamo sapere la velocità della particella (e viceversa). Nella formula precedente il simbolo h è lo stesso incontrato nella descrizione della radiazione di corpo nero. Il fatto rilevante è che il prodotto Δx Δ(mv) non può mai annullarsi, quindi per nessuna delle variabili in esame la sua incertezza può essere ridotta a zero. Ci troviamo quindi di fronte ad una proprietà del mondo quantistico, ossia che interessa il microcosmo, completamente nuova e sconvolgente. Come accennato, il principio ci permette di capire perchè scompare la figura di interferenza se provassimo a deteminare attraverso quale fenditura è passato l'elettrone. Per ottenere tale informazione, quello che dovremmo fare è “vedere” gli elettroni in qualche modo. Ora, la luce visibile non è sufficiente, perchè la risoluzione spaziale che potremmo raggiungere con tali sonde è troppo bassa per poter risolvere il minuto elettrone. Allora dobbiamo usare delle radiazioni piu' potenti, quali i raggi X, da inviare in prossimita delle fenditure. L'effetto Compton, però, ci dice che parte della energia dei fotoni viene trasmessa agli elettroni che repentinamente cambiano la loro velocità e quindi si comportano come particelle; è chiaro, allora, che essi hanno perso le caratteristiche ondulatorie e quello che si osserva sullo schermo è una distribuzione di elettroni in accordo con il fatto che un po' passano per una fenditura e un po' nell'altra. Potremmo ovviare a tale problema inviando onde elettromagnetiche di frequenza talmente bassa da non disturbare il moto degli elettroni. In questo caso la figura di interferenza rimane. Tuttavia, abbiamo ceduto all'elettrone una quantità Δ(mv) molto piccola e, in accordo con Heisenber, abbiamo completamente perso informazione su Δx, che ora è una quantità grande come si vede invertendo la formula (1).
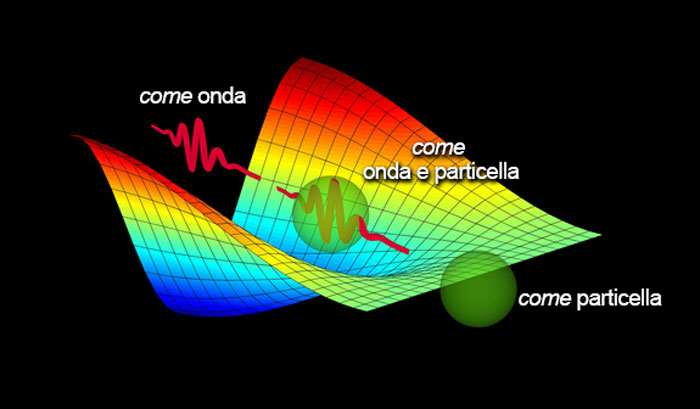 |
| Fig. 7 Dualismo onda-particella |
Quindi, nel momento in cui si è cercato di rilevare la natura ondulatoria degli elettroni abbiamo perso la figura di interferenza, mentre quando l'abbiamo lasciata inalterata abbiamo perso l'informazione sulla fenditura attraversata. Il comportamento dell'elettrone nel caso in esame non ha, ovviamente, un analogo nel mondo macroscopico in cui viviamo; pertanto, si preferisce parlare di elettrone come di un oggetto quantistico, riferendoci con cio' alla proprietà di essere descritto come onda o come particella a seconda dei casi. Il limite tra mondo macroscopico e mondo quantistico non è ben definito; nella vita quotidiana non ci aspettiamo per una pallina da tennis un comportamento ondulatorio cosi come non ce lo aspettiamo per un pallone da calcio o un essere umano. La spiegazione potrebbe essere che tali oggetti (macroscopici) interagiscono istantaneamente con l'ambiente circostante e quindi il collasso della loro funzione d'onda è un fenomeno che avviene molto prima che si possano sviluppare proprietà quantistiche. Esistono molecole (anche relativamente grandi) per le quali gli effetti quantistici giocano un ruolo predominante, ma quale sia la dimensione minima di un oggetto al di sopra della quale il suo comportamento può essere descritto dalla fisica classica è molto difficile da stabilire.
Cenni di Bibliografia
[1] Silvia Arrojo Camejo, “Il bizzarro mondo dei quanti”, Springer.
[2] Manjit Kumar, “Quantum”, Icon Books Ltd, 2009.

