 La determinazione delle distanze dei corpi celesti è certamente uno dei problemi piu interessanti e più significativi dell'astronomia. Di metodi per il calcolo della distanza ne esistono numerosi tipi e si distinguono sostanzialmente per la "profondità" che riescono a raggiungere . Per le distanze relativamente prossime a noi, quindi nel sistema solare o per le stelle più vicine, si possono utilizzare metodi geometrici quale quello della parallasse  . Per distanze superiori esistono sistemi che sfruttano le proprietà fisiche delle stelle e dei sistemi stellari, andando a individuare la cosiddetta "candela standard"  [64]. Uno dei metodi che si utilizzano è quello basato sulla relazione luminosità-tempo delle stelle cefeidi: un tipo di stelle variabili  che prendono il nome dalla stella delta della costellazione del Cefeo la cui luminosità varia del 50% in cinque giorni.
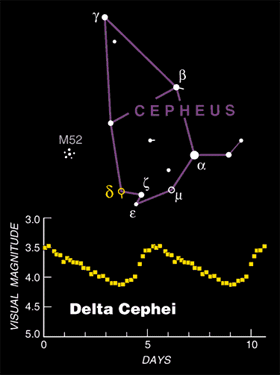
Delta Cephei
(grafico dal sito http://skyandtelescope.com)
Negli anni a cavallo tra ‘800 e ‘900 l’astronoma americana Henrietta Swan Leavitt  si dedicò alle osservazioni delle stelle variabili cefeidi della Grande e della Piccola Nube di Magellano  , in qualità di capo del dipartimento di fotometria fotografica dell’Harvard College Observatory.
Nel corso della sua carriera la Leavitt scoprì oltre 2.400 stelle variabili, circa la metà di quelle conosciute a quell’epoca. I risultati delle sue osservazioni, pubblicati nel 1912, mostrarono che stelle cefeidi le cui variazioni di luminosità avevano un periodo diverso, avevano anche una diversa magnitudine (cioè erano più o meno luminose).  Appartenendo tutta alla stessa struttura (una delle Nubi di Magellano) ed essendo quindi tutte alla stessa distanza, la maggiore o minore magnitudine poteva essere legata soltanto alla diversa lunghezza del periodo di variabilità delle diverse stelle. In particolare, costruendo un grafico che riportasse su un asse (asse x, delle ascisse) la magnitudine assoluta (calcolata a partire dalla magnitudine apparente osservata e dalla distanza delle Nubi di Magellano, all’epoca già nota) e sull’altro (asse y, asse delle ordinate) il logaritmo del periodo di variabilità, la Leavitt osservò che le stelle si disponevano, con buona approssimazione, lungo una linea retta.
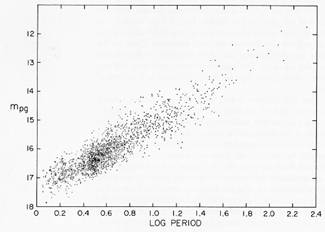
Ecco dunque l’origine della formula M = A + B log P, dove B è il coefficiente angolare della retta individuata sul grafico e A è il valore di ordinata (quindi di magnitudine) al quale la retta interseca l’asse verticale del grafico: i valori esatti furono all’epoca ricavati proprio dal grafico stesso, attraverso l’analisi della retta lungo cui si disponevano i punti che rappresentavano le stelle. Non è facile trovare dei precisi riferimenti su quali furono le intuizioni che portarono la Leavitt a correlare la magnitudine e il periodo di variabilità delle cefeidi; ma d’altra parte anche la genesi del famoso diagramma H-R , dovuto agli astronomi Hertzsprung  e Russell , che, mettendo in relazione temperatura e luminosità, è diventato uno dei capisaldi di riferimento per l’evoluzione stellare, è ammantata di una certa dose di casualità. Probabilmente, in entrambi venne effettuata una lunga serie di tentativi prima di arrivare al risultato. La formula ricavata dalla Leavitt è stata poi accuratamente calibrata e attraverso di essa, una volta calcolato con le osservazioni il periodo di variabilità, si può ricostruire la magnitudine assoluta di una cefeide; confrontando quest’ultima con la magnitudine apparente osservata, si può calcolare la distanza della stella. Prima dei calcoli della Leavitt, si potevano calcolare le distanze stellari fino a circa 100 anni-luce : grazie al lavoro dell’astronoma americana si aprì la strada per calcolare distanze fino a 10 milioni di anni-luce, cioè 100.000 volte più lontano.
Paolo Ferretti – Astrofilo
|
