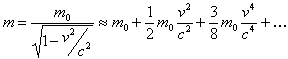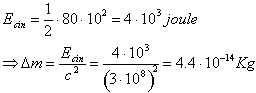La famosa equivalenza di Einstein La famosa equivalenza di Einstein  tra massa ed energia totale implica, come suppone correttamente il nostro web-nauta, che nel sistema di riferimento tra massa ed energia totale implica, come suppone correttamente il nostro web-nauta, che nel sistema di riferimento  del laboratorio un corpo in moto abbia una massa maggiore di quando è fermo. Occorre ricordare che la massa del laboratorio un corpo in moto abbia una massa maggiore di quando è fermo. Occorre ricordare che la massa  [106] di un corpo è definita operativamente dal rapporto tra una forza e l’accelerazione che il corpo riceve sotto l’ azione della forza [106] di un corpo è definita operativamente dal rapporto tra una forza e l’accelerazione che il corpo riceve sotto l’ azione della forza  , quindi m=F/a. Questa semplice equazione, insieme al dato sperimentale che la velocità della luce , quindi m=F/a. Questa semplice equazione, insieme al dato sperimentale che la velocità della luce 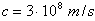 non può essere superata non può essere superata  [76] [76]  [111] [111]  [66] inglobato nella relatività ristretta [66] inglobato nella relatività ristretta  , permette di capire qualitativamente che la massa di un corpo in moto è tanto maggiore quanto più questo si avvicina alla velocità della luce: per non superare c la variazione di velocità nell’unità di tempo, cioè l’accelerazione , permette di capire qualitativamente che la massa di un corpo in moto è tanto maggiore quanto più questo si avvicina alla velocità della luce: per non superare c la variazione di velocità nell’unità di tempo, cioè l’accelerazione  , deve tendere a zero e quindi la massa m=F/a tende all’ infinito. La relazione tra la massa di un corpo e la sua velocità, come si ricava nella teoria della relatività, è : , deve tendere a zero e quindi la massa m=F/a tende all’ infinito. La relazione tra la massa di un corpo e la sua velocità, come si ricava nella teoria della relatività, è :
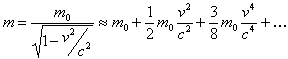
E' importante notare che nel caso v < < c, in cui è possibile trascurare il termine ~v4, nell’espressione dell’ energia totale si ottiene la consueta espressione per l’ energia cinetica:
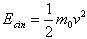 Il termine \(m_0 c^2\) è un termine costante, corrispondente alla massa di riposo del corpo, e non ha alcun effetto sul moto. Il termine \(m_0 c^2\) è un termine costante, corrispondente alla massa di riposo del corpo, e non ha alcun effetto sul moto.
Nel caso numerico presentato dal nostro web-nauta abbiamo:
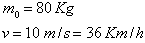
Da questi valori risulta quindi :
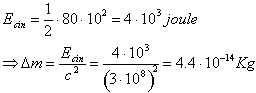
L’ incremento di massa corrispondente alle velocità ordinarie è, come si vede, estremamente piccolo. Un corpo che si muovesse a 0.1 c (un decimo della velocità della luce) avrebbe appena \(\Delta m\) = 0.5 %.
Piero Patteri – Fisico
|