Ho alcuni dubbi a proposito dell'orbita ellittica seguita dalla Terra nel suo giro intorno al Sole. Ho letto che l'orbita è determinata dalla risultante di due forze, la forza gravitazionale del Sole che attira la Terra verso di se e la forza rappresentata dal momento angolare della Terra (momento angolare dato da massa * velocità * raggio) ora dunque la risultante di queste due forze mi da la traiettoria seguita dalla Terra, se fin qui ho sbagliato qualcosa viene a cadere il senso della mia domanda). Tutto questo ragionamento mi è chiaro fin quando immagino una traiettoria circolare, la forza attrattiva del Sole è sempre la stessa, la massa della Terra, la sua velocità ed il raggio rimangono inalterati e le due forze si equilibrano permettendo un moto circolare. I guai (per me) cominciano se considero l'orbita ellittica...Immaginiamoci ad esempio la Terra nel momento in cui si trova più vicino al Sole, la forza gravitazionale del Sole è X e il momento angolare è Y per cui poi la risultante da come detto prima una certa direzione. Ma se poi succede che la Terra se pur lentamente comincia ad allontanarsi, deve verificarsi che: o il valore della X diminuisca un pochino, oppure che il valore della Y aumenti un pochino. D'altra parte si sa che esiste un principio detto della conservazione del momento angolare, per cui questo momento angolare appunto è sempre uguale in qualsiasi punto dell'orbita. Per cui esclusa la possibilità che aumenti questo momento angolare, rimarrebbe che dovrebbe diminuire la forza gravitazionale del Sole...e come può succedere tutto questo? (Nello)
Nota redazionale SxT
Questo argomento è stato già trattato in due precedenti risposte fornite ai web-nauti Luca 
[244] e Francesco [49], come anche quelle fornita alla domanda di Antonella pubblicata in questo stesso mese mese [310] .
L’ellisse è un tipo di conica definita come luogo dei punti O la cui somma delle distanze da due punti fissi F1 e F2, detti fuochi, è costante (fig.1). Su questa regola si basa il metodo del giardiniere
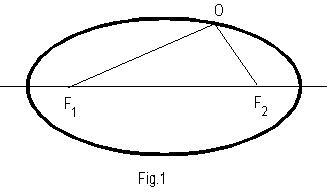per costruire delle aiuole ellittiche. Basta prendere una cordicella legata a due pioli, conficcati nei fuochi, e avente la lunghezza costante OF1+ OF2. La punta O di un terzo piolo, che viene fatto scorrere lungo lo spago teso, traccerà sul terreno una curva ellittica. E’ verificabile che le varie coniche si possono ottenere tagliando un cono a doppia falda con un piano inclinato opportunamente. Si può fornire, inoltre, una definizione unitaria di conica come insieme di punti le cui distanze da un fuoco e da una retta (direttrice) sono in un rapporto costante ε (eccentricità). Se ε=0, ε=0<1, ε=1, ε>1 la conica diventa rispettivamente una circonferenza, un’ellisse, una parabola, un ramo d’iperbole. Questa definizione viene rappresentata analiticamente mediante un’equazione in coordinate polari.
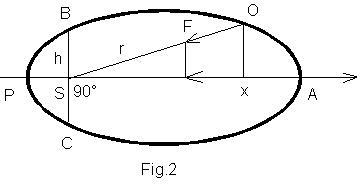Utilizzando la seguente equazione delle coniche (*) : ρ= h+εx (fig.2), in cui x è l’ascissa di O, ρ è la distanza di O dall’origine di x, ρ = h , la precedente formula, oltre ad essere unitaria per le varie coniche, offre altri vantaggi:
* è una semplice relazione lineare tra ρ e x;
* non contiene funzioni trigonometriche;
* utilizza una coordinata x cartesiana e un’altra polare ρ con la stessa origine sovrapposta ad uno dei fuochi;
* permette di risolvere facilmente alcuni problemi fisici.
In questo sistema misto cartesiano-polare, l’equazione delle coniche ha una forma lineare e riproduce metà curva, simmetrica alla parte rimanente rispetto a x. Non mi dilungherò sulle proprietà di questa formulazione, perché quanto detto è una premessa sufficiente per rispondere al quesito sul moto del pianeta O, che descrive un’ellisse intorno al sole S situato in uno dei fuochi della curva. Svilupperò l’argomento di livello universitario e particolarmente ostico, utilizzando ulteriori ricerche didattiche personali. Per semplicità O ed S verranno considerati puntiformi con la massa di O trascurabile nei confronti di quella di S. O viene attratto da S con una forza F nella direzione OS, la cui proiezione sull’asse x vale -Fx/ρ, che rapportata alla massa m di O porge la sua accelerazione ax lungo x . L’accelerazione dovuta al cambiamento del valore del raggio risulta aρ = ε ax,dato che h ed ε sono costanti nell’espressione di ρ=h+εx; ne segue che mρ=-Fe x/r=fda cui discende che l’accelerazione aρ è negativa per x>0 cioè nel percorso CAB ed è positiva per x<0 ovvero nel tratto BPC. In punti simmetrici rispetto a x le aρ hanno uguali valori, che in particolare si annullano in B e C perché ivi è x = 0. Nel moto circolare uniforme (ε = 0) è costante ρ e quindi diventa nulla la velocità radiale ed anche aρ. Nel moto di O in senso antiorario sull’ellisse, la distanza ρ diminuisce sull’arco ABP e aumenta sulla curva PCA, dove A (afelio) e P (perielio) sono, rispettivamente, i punti più lontano e vicino al sole. La velocità radiale Vρ di avvicinamento dal valore nullo in A aumenta fino a B e diminuisce da B a P ove ritorna a zero. Sull’arco successivo la Vρ di allontanamento cresce fino a C e poi decresce sino ad A. Da ciò emerge che l’accelerazione aρ è diretta verso S (aρ< 0) per x > 0, è uscente da S (aρ>0) per x<0, è nulla per x=0 in conformità alle considerazioni precedenti. Il comportamento di O può essere più agevolmente inteso ponendosi nel sistema di riferimento che ruota attorno ad S assieme ad O. Per cogliere subito l’osservazione, basta segnare su un sottile bastoncino b, rotante attorno ad un estremo situato in S, i punti O dell’ellisse che b interseca. In questo sistema la traiettoria di O è il segmento PA di andata e ritorno allineato con S e la sua accelerazione aρ è prodotta dalla forza f, orientata verso S nel percorso CAB ed in senso contrario nel cammino BPC (fig.3).
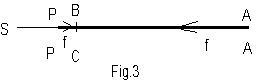Questa forza fornisce al pianeta O un richiamo verso il punto B coincidente con C. Il punto O oscilla sul segmento PA ed ha una velocità relativa nulla agli estremi A e P nei quali deve invertire il suo moto. Da A a B, la f imprime un incremento al modulo della velocità relativa fino ad un massimo in B, dove la forza è zero. Da B a P la massa viene contrastata dalla forza, che ne abbassa la velocità fino a ridurla a zero in P. Ora la f provvede a ribaltare ed innalzare la velocità fino ad un massimo in C, in cui f si annulla. Il corpo oltrepassa C, proseguendo verso A, ostacolato dalla forza f, che fa decrescere la velocità sino al valore nullo in A. Il tragitto APA viene, così, completato ed il ciclo continuerà a ripetersi. Soltanto per l’azione del richiamo e non per l’espressione della forza, un moto similare ma simmetrico è quello provocato da una molla elastica, che produce con la sua forza (diretta sempre verso un centro N) delle oscillazioni tra due punti con velocità crescente nel moto verso N e calante nello spostamento verso gli estremi della traiettoria. Se la molla, invece di esplicare una forza proporzionale e discorde alla sua variazione di lunghezza, riproducesse la f planetaria, le vibrazioni sarebbero uguali a quelle di O sul segmento PA. Dall’equazione dell’ellisse si ha εx = ρ-h e dunque maρ = -F+Fh/ρ; allora nel sistema rotante la forza complessiva ha una componente attrattiva –F ed un repulsiva Fh/ρ. Nella modalità delineata dall’estensore del quesito, il comportamento del corpo si può imputare a due forze radiali antagoniste: gravitazionale reale e centrifuga apparente. Nel moto circolare uniforme si ha ρ = h, da cui scaturisce che le due forze si equilibrano perfettamente. Anche nei punti C e B dell’ellisse (ρ = h) queste due forze si annullano. Nel percorso CAB (ρ > h) prevale la forza gravitazionale su quella centrifuga con un risultante rivolta verso S. Sull’arco BPC (ρ< h) è preponderante invece l’azione centrifuga rispetto a quella gravitazionale con una risultante uscente da S.
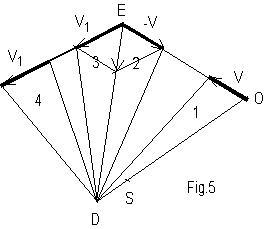
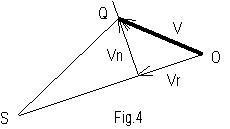L’accelerazione aρ ha il verso della forza risultante, negativa in CAB e positiva in BPC come già stabilito. Perché si conserva il momento angolare L di cui parla il nostro web-nauta? L del pianeta rispetto ad S vale mρVn, dove Vn è la componente della velocità ortogonale al raggio, e risulta anche 2mk in cui k è rappresentata dall’area del triangolo SOQ, denominata velocità areale di O intorno ad S (fig.4). Nel moto dei pianeti la forza reale punta sempre verso S ed è detta centrale. Da questa ipotesi discende che la velocità areale ed il momento angolare si mantengono costanti durante il moto. Consegue che la Vn diminuisce procedendo dal perielio all’afelio e cresce da A a P. Sulla circonferenza la Vn=V è costante perché lo è r e ciò significa che il moto è pure uniforme. Tra le diverse dimostrazioni didattiche che ho ottenuto per la costanza di k, reputo efficace, precisa e semplice la spiegazione geometrica seguente. Siano v e v1 due velocità consecutive di O con le rette d’azione che si intersecano in E (fig.5). In E si riportino v1 e –v e si trovi la loro risultante, che indica la variazione di velocità. Sia D il punto d’intersezione tra la giacitura della suddetta variazione e la semiretta OS. Le aree dei triangoli 1 e 4 sono le velocità areali k e k1 del pianeta intorno a D in due istanti successivi. Le aree 1 e 2 sono uguali perché hanno le basi v e la stessa altezza. Analogamente sono uguali le aree 3 e 4. Le aree 2 e 3, a loro volta, sono uguali poiché hanno le medesime altezze rispetto alla stessa base ED. Si desume che le quattro aree sono uguali e quindi k = k1. Ma quando l’intervallo di tempo diventa infinitesimo, la variazione di velocità si dispone nella direzione dell’accelerazione e, dunque, della forza gravitazionale istantanea che passa per il polo S. Si arguisce che le velocità areali rispetto a S dopo un tempo infinitesimo sono uguali. Dal momento che il discorso si può iterare per tutti gli istanti successivi, si conclude che il moto di O sull’ellisse, imposto dalla forza gravitazionale, si svolge con velocità areale e con momento angolare costanti attorno ad S.
La forza centrifuga mVn2/ρ = 4k2m/ρ3 effettivamente è legata alla velocità areale o al momento angolare, ma la sua variazione nel movimento sull’ellisse è affidata all’inversa proporzionalità al cubo di ρ. Come si concilia questa formula con la forza centrifuga Fh/ρ, che deriva dall’equazione della traiettoria e dalla sollecitazione gravitazionale? La legge di gravitazione universale afferma che F = GMm/ρ2, ove G = 6,67 10-11 Nm2/kg2 ed M è la massa del sole. Uguagliando le due espressioni della forza centrifuga si ricava che h = 4k2/(GM). Ciò verifica che l’ellisse soddisfa l’equazione del moto purchè h abbia il valore summenzionato. Rimane da spiegare perché l’unica forza fittizia che influenza il moto sia quella centrifuga data dalla formula mVn2/ρ. La velocità si può scomporre in due componenti Vn e Vρ perpendicolare e parallela ad ρ rispettivamente (fig.4). Ogni componente dà luogo a due accelerazioni, orientate rispetto al vettore di partenza, parallelamente per la variazione del modulo e ortogonalmente nel verso di rotazione per il cambiamento di direzione. Si ottengono quattro componenti dell’accelerazione di cui le due perpendicolari ad SO si devono neutralizzare perché la forza gravitazionale, essendo centrale, agisce nella direzione OS. Rimangono soltanto le componenti radiali aρ procurata dalla variazione del modulo di Vρ e centripeta -Vn2/ρ provocata dalla rotazione di Vn. Perciò l’accelerazione complessiva a = aρ - Vn2/ρ e quindi maρ = -F + mVn2/ρ. Nel sistema di riferimento rotante aρ è l’accelerazione relativa, -F = ma è la forza gravitazionale e mVn2/ρ è la forza centrifuga come volevasi verificare.
Pasquale Catone – Docente di Fisica
(1) P. Catone, Una deduzione didattica della legge di forza che trattiene i corpi su orbite coniche…, La Fisica nella Scuola, 2, 1979.
revisione G. Chiarelli marzo 2020