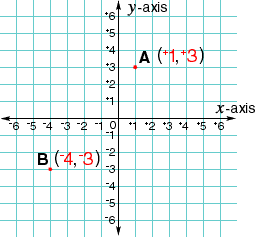Le tre leggi che Keplero Le tre leggi che Keplero  scoprì, sono il frutto del lavoro svolto dallo scenziato tedesco per inquadrare la grande quantità di osservazioni fatte dal suo maestro Tycho Brahe scoprì, sono il frutto del lavoro svolto dallo scenziato tedesco per inquadrare la grande quantità di osservazioni fatte dal suo maestro Tycho Brahe  nella concezione eliocentrica dell’Universo di Copernico nella concezione eliocentrica dell’Universo di Copernico  , cioè con il Sole al centro dell’Universo e i pianeti e la Terra in moto attorno ad esso. I dati sperimentali (le osservazioni) raccolti da Brahe , cioè con il Sole al centro dell’Universo e i pianeti e la Terra in moto attorno ad esso. I dati sperimentali (le osservazioni) raccolti da Brahe  erano così numerosi e precisi da permettere a Keplero di formulare le tre leggi, che per questo si possono definire fenomenologiche erano così numerosi e precisi da permettere a Keplero di formulare le tre leggi, che per questo si possono definire fenomenologiche , nel senso che ammettendo la validità di esse, le osservazioni delle posizioni dei pianeti fatte nel passato concordavano perfettamente con quanto calcolato utilizzando le tre leggi; non solo, si potevano anche calcolare le posizioni dei pianeti nel futuro, e quindi in conclusione, conoscere il moto dei pianeti attorno al Sole. In effetti, come dice il nostro web-nauta, è facile dimostrare la seconda e la terza legge di Keplero; infatti la seconda si può ricavare imponendo la conservazione del momento angolare , nel senso che ammettendo la validità di esse, le osservazioni delle posizioni dei pianeti fatte nel passato concordavano perfettamente con quanto calcolato utilizzando le tre leggi; non solo, si potevano anche calcolare le posizioni dei pianeti nel futuro, e quindi in conclusione, conoscere il moto dei pianeti attorno al Sole. In effetti, come dice il nostro web-nauta, è facile dimostrare la seconda e la terza legge di Keplero; infatti la seconda si può ricavare imponendo la conservazione del momento angolare   [140] del sistema, mentre la terza è una conseguenza del principio di conservazione dell’energia [140] del sistema, mentre la terza è una conseguenza del principio di conservazione dell’energia  [100] [100] [317]. Ricordiamo che la prima legge di Keplero afferma: le orbite dei pianeti sono ellittiche e il Sole occupa uno dei fuochi [317]. Ricordiamo che la prima legge di Keplero afferma: le orbite dei pianeti sono ellittiche e il Sole occupa uno dei fuochi  . Il nostro web-nauta ci chiede come ha fatto Keplero a determinare che le orbite dei pianeti sono delle ellissi . Il nostro web-nauta ci chiede come ha fatto Keplero a determinare che le orbite dei pianeti sono delle ellissi  in cui il Sole occupa uno dei fuochi. Ebbene, come detto prima, Keplero ha messo in accordo i dati sperimentali con una ipotesi empirica non dedotta da leggi consolidate. Egli ha supposto che le orbite fossero ellittiche, e questa supposizione è stata sufficiente. Tutte le osservazioni sperimentali delle posizioni dei pianeti si accordano infatti con questa ipotesi. in cui il Sole occupa uno dei fuochi. Ebbene, come detto prima, Keplero ha messo in accordo i dati sperimentali con una ipotesi empirica non dedotta da leggi consolidate. Egli ha supposto che le orbite fossero ellittiche, e questa supposizione è stata sufficiente. Tutte le osservazioni sperimentali delle posizioni dei pianeti si accordano infatti con questa ipotesi.
 Che l’orbita di un pianeta sia ellittica Che l’orbita di un pianeta sia ellittica  [49], [49], [244], [244], [310] si può dimostrare in realtà utilizzando la legge di attrazione gravitazionale [310] si può dimostrare in realtà utilizzando la legge di attrazione gravitazionale  scoperta da Isaac Newton scoperta da Isaac Newton
\[F=\frac{GmM}{r^2}\]
dove G  [322], [322],  [102] è la costante di gravitazione universale, m ed M sono le masse dei corpi (nel caso astronomico del satellite e del Sole) ed r indica la distanza che le separa, unitamente alla seconda legge del moto (F = ma, dove "a" è l'accelerazione). Ciò, comunque, è un risultato successivo. In pratica Keplero non aveva dimostrato che le orbite sono delle ellissi: egli aveva scoperto che le osservazioni sperimentali si potevano spiegare facendo tale ipotesi. Utilizzando le leggi di Newton (gravitazione e seconda legge del moto) si può invece far derivare da esse che le orbite sono effettivamente delle ellissi. La dimostrazione è abbastanza complessa e richiede conoscenze nel campo della matematica superiore (derivazione e integrazione di funzioni, calcolo infinitesimale, risoluzione di equazioni differenziali, trattazione del problema in coordinate polari). Tuttavia, posso tentare di illustrare il percorso che si segue per dimostrare che l’orbita è una ellisse [102] è la costante di gravitazione universale, m ed M sono le masse dei corpi (nel caso astronomico del satellite e del Sole) ed r indica la distanza che le separa, unitamente alla seconda legge del moto (F = ma, dove "a" è l'accelerazione). Ciò, comunque, è un risultato successivo. In pratica Keplero non aveva dimostrato che le orbite sono delle ellissi: egli aveva scoperto che le osservazioni sperimentali si potevano spiegare facendo tale ipotesi. Utilizzando le leggi di Newton (gravitazione e seconda legge del moto) si può invece far derivare da esse che le orbite sono effettivamente delle ellissi. La dimostrazione è abbastanza complessa e richiede conoscenze nel campo della matematica superiore (derivazione e integrazione di funzioni, calcolo infinitesimale, risoluzione di equazioni differenziali, trattazione del problema in coordinate polari). Tuttavia, posso tentare di illustrare il percorso che si segue per dimostrare che l’orbita è una ellisse  (o una conica (o una conica  in generale in generale  ). Si parte dal descrivere il problema in coordinate ). Si parte dal descrivere il problema in coordinate  polari: anziché utilizzare le coordinate x e y di un piano cartesiano per descrivere il moto del punto materiale (pianeta), si utilizzano le coordinate polari: anziché utilizzare le coordinate x e y di un piano cartesiano per descrivere il moto del punto materiale (pianeta), si utilizzano le coordinate  polari: la posizione del punto materiale viene quindi individuata da una coppia di numeri: la distanza r da un punto origine e l’angolo q che la congiungente con l’origine forma con l’asse orizzontale (quello delle x per capirci). L’utilizzo di coordinate polari permette di semplificare i calcoli. Coordinate Polari: polari: la posizione del punto materiale viene quindi individuata da una coppia di numeri: la distanza r da un punto origine e l’angolo q che la congiungente con l’origine forma con l’asse orizzontale (quello delle x per capirci). L’utilizzo di coordinate polari permette di semplificare i calcoli. Coordinate Polari:
|
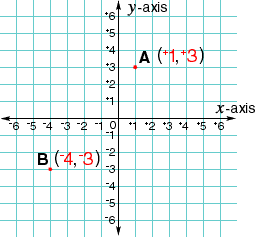
Coordinate Cartesiane
|
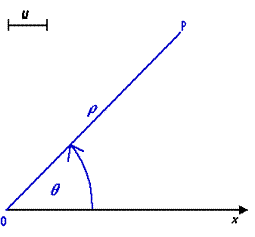
Coordinate Polari
|
Si calcolano la derivata prima rispetto al tempo del vettore  posizione r (individuato dal modulo di r e dall'angolo q) che è la velocità, e la derivata seconda rispetto al tempo del vettore r, che è l’accelerazione. Successivamente, imponendo alcune condizioni tipiche del moto in esame, per esempio che l’accelerazione è sempre diretta lungo il vettore r in quanto la forza è diretta verso il centro, imponendo che la forza (massa x accelerazione) sia uguale alla forza gravitazionale GmM/r2, e usando tecniche tipiche dell’analisi matematica si arriva ad una equazione del moto che ha la forma seguente: posizione r (individuato dal modulo di r e dall'angolo q) che è la velocità, e la derivata seconda rispetto al tempo del vettore r, che è l’accelerazione. Successivamente, imponendo alcune condizioni tipiche del moto in esame, per esempio che l’accelerazione è sempre diretta lungo il vettore r in quanto la forza è diretta verso il centro, imponendo che la forza (massa x accelerazione) sia uguale alla forza gravitazionale GmM/r2, e usando tecniche tipiche dell’analisi matematica si arriva ad una equazione del moto che ha la forma seguente:
r = Costante / (1 + e cosq) che è l’equazione di una conica, nella fattispecie:
di una ellisse (se il parametro eccentricità e è compreso tra 0 e 1),
di una parabola (se e=1),
di una iperbole (se e>1),
di un cerchio (se e=0).
E’ da notare che in natura si hanno orbite ellittiche con relativamente piccola eccentricità  (quelle dei pianeti del sistema solare, o di altri sistemi), orbite con grande eccentricità (comete periodiche che danno sfoggio di sé durante il loro avvicinamento al sole, per poi allontanarsi per decenni o centinaia di anni), ma anche orbite paraboliche (quelle dei pianeti del sistema solare, o di altri sistemi), orbite con grande eccentricità (comete periodiche che danno sfoggio di sé durante il loro avvicinamento al sole, per poi allontanarsi per decenni o centinaia di anni), ma anche orbite paraboliche  o iperboliche o iperboliche  (comete che dopo un solo passaggio non vengono catturate dal sistema solare e non faranno mai ritorno). (comete che dopo un solo passaggio non vengono catturate dal sistema solare e non faranno mai ritorno).
Sandro Barbanera – Fisico
|