 La bottiglia di Klein, descritta nel 1882 dal matematico tedesco Felix Klein  , è un' entità matematica molto particolare, e si distingue da altri oggetti normali appartenenti alla sua stessa specie, ovvero la famiglia delle varietà differenziabili  . La varietà differenziabile tende a generalizzare il concetto di superficie, o di curva, nell’ottica di studiare la geometria di curve e superfici che, in un certo senso non esistono in natura, cioè non necessariamente sono definibili in uno spazio naturale .
Una superficie ordinaria (per esempio un cilindro, o una sfera) immersa nel comune spazio euclideo a tre dimensioni ha sempre due facce, un sopra ed un sotto. Se supponiamo di colorare un lato della superficie, per colorare il lato opposto dobbiamo per forza attraversare il bordo della superficie stessa. Nel caso della sfera inoltre la superficie è anche chiusa, e quindi c'è un dentro ed un fuori, e non possiamo colorare la faccia interna della superficie sferica stando al di fuori. Dobbiamo pensare di “bucare” la superficie stessa ed entrarci. Questo accade per le superfici naturali, dette anche orientabili. In matematica però esistono superfici che non orientabili, ovvero superfici che non hanno due facce, non hanno un sopra ed un sotto, non hanno un dentro ed un fuori. L’esempio più noto è il cosiddetto nastro di Möbius .
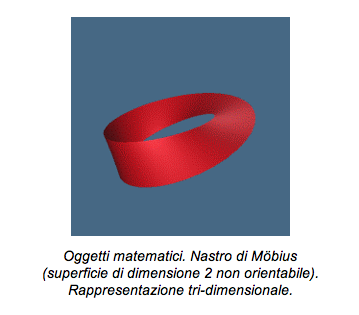
Si tratta di una superficie ad una sola faccia ed un solo bordo, tale cioè che - seguendo una linea continua senza attraversare il bordo - si può raggiungere qualsiasi punto della figura (da cui si comprende la definizione di non orientabili  che in matematica si associa a questo tipo di superfici). La situazione è diversa da quella di un foglio (superficie orientabile), che possiede due facce separate tra loro da un bordo che bisogna attraversare per passare da una faccia all’altra. Il nastro di Möbius si sviluppa in due dimensioni ma – ovviamente - superfici non orientabili possono essere costruite in spazi di qualunque numero di dimensioni. Un esempio noto di superficie di questo tipo è la bottiglia di Klein, che di per sé è di dimensione 4. Esistono vari modi tentativi di rappresentare oggetti in uno spazio di n dimensioni in un numero di dimensioni inferiore esperto 184 a n. Nel caso della bottiglia di Klein si può immaginare nello spazio tridimensionale, tramite una procedura mentale di distorsione, d’uso comune in topologia : basta immaginare di prendere una normale bottiglia, allungarne il collo, piegarlo e farlo penetrare nel fianco della bottiglia stessa, fino a farlo uscire sul fondo. Tale auto-intersezione non si vedrebbe se potessimo rappresentare la superficie in dimensione 4, ma siamo costretti a utilizzarla per raffigurarla in dimensione 3  .
Ecco una foto che mostra cosa si ottiene. La bottiglia di Klein è una superficie chiusa, come la sfera (infatti non ha un bordo), ma non ha un dentro ed un fuori: infatti se riempiamo la bottiglia reale raffigurata di sopra con del liquido, rigirando la bottiglia stessa il liquido uscirà: il che è impossibile per una normale superficie chiusa come la superficie sferica. Esistono altri tipi di superfici non orientabili, alcuni più semplici come ad esempio il nastro di Möbius altri più complessi Per una discussione più approfondita i nostri web-nauti trovano dalla rubrica Scaffali un interessante approfondimento da scaricare su questo tipo di simili oggetti matematici curiosi.
Luca Lussardi – Matematico
|
