Quando una nube interstellare inizia a contrarsi, inizia ad aumentare la temperatura e a emettere radiazioni, fino ad arrivare a emettere nell’infrarosso. Ora mi chiedo, se non ci sono ancora reazioni di fusione, l’energia che fa aumentare la temperatura delle nube in contrazione è l’energia gravitazionale? E come si calcola l’energia in ballo? È giusto applicare la formula E = -3/5 GM2 / R per calcolare l’energia di legame gravitazionale che si ha prima e dopo la contrazione? (Silvia)
Il modo classico di stimare l’energia in ballo è quello di utilizzare il cosiddetto Teorema del Viriale, secondo cui l’energia cinetica media K di un sistema all’equilibrio è uguale a -1/2 della sua energia potenziale media V:
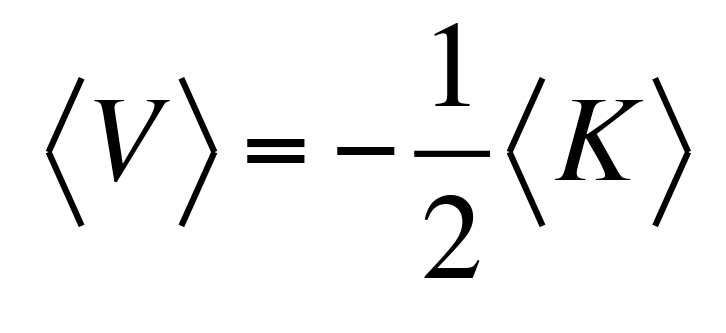
Se quindi si considera l’energia totale media
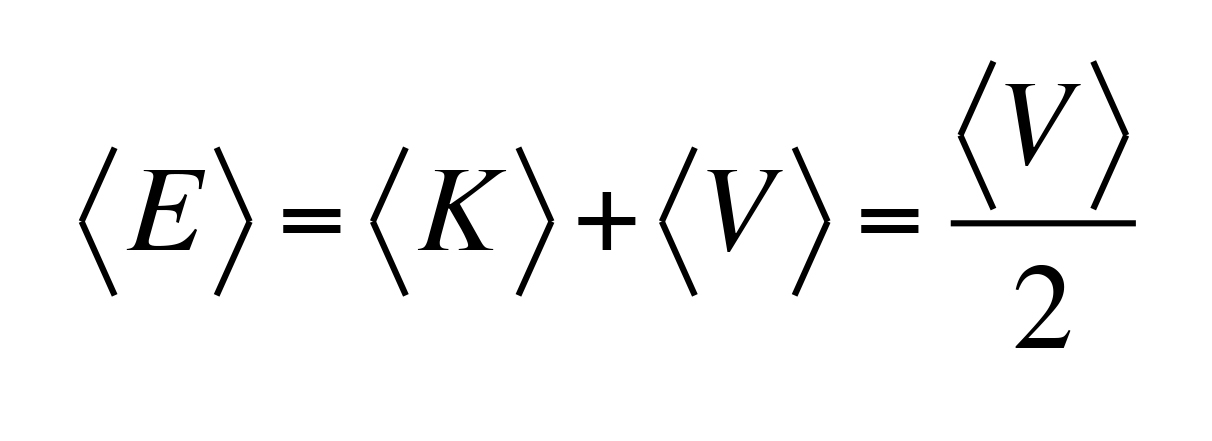
che ci dice che in un collasso gravitazionale, metà dell’energia potenziale viene convertita in energia cinetica delle particelle di gas, che quindi si scalda, mentre l’altra metà è disponibile per essere radiata sotto forma di radiazione elettromagnetica.
Per esempio, prendiamo una nube di gas (monatomico) di massa M e con raggio R e densità uniforme e calcoliamo quanta energia viene radiata quando questa collassa fino ad avere un raggio R. L’energia potenziale di una sfera uniforme di massa M e raggio R si calcola essere, in generale:
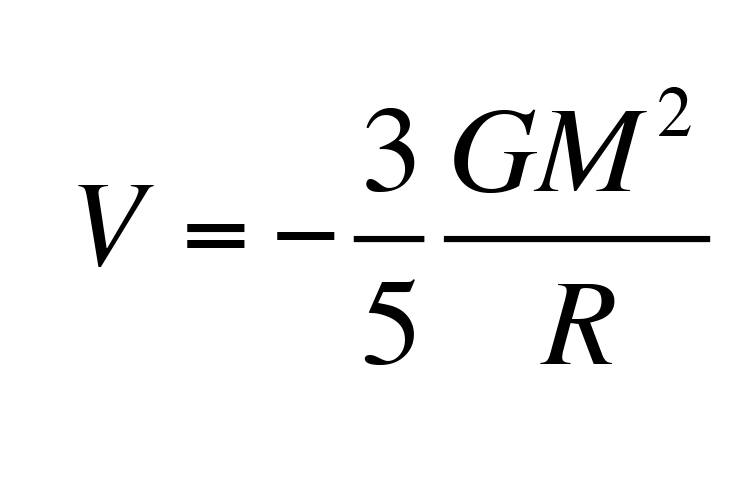
Quindi quando il raggio R è molto grande, V ~ 0 e l’energia totale media acquisita dal sistema è:
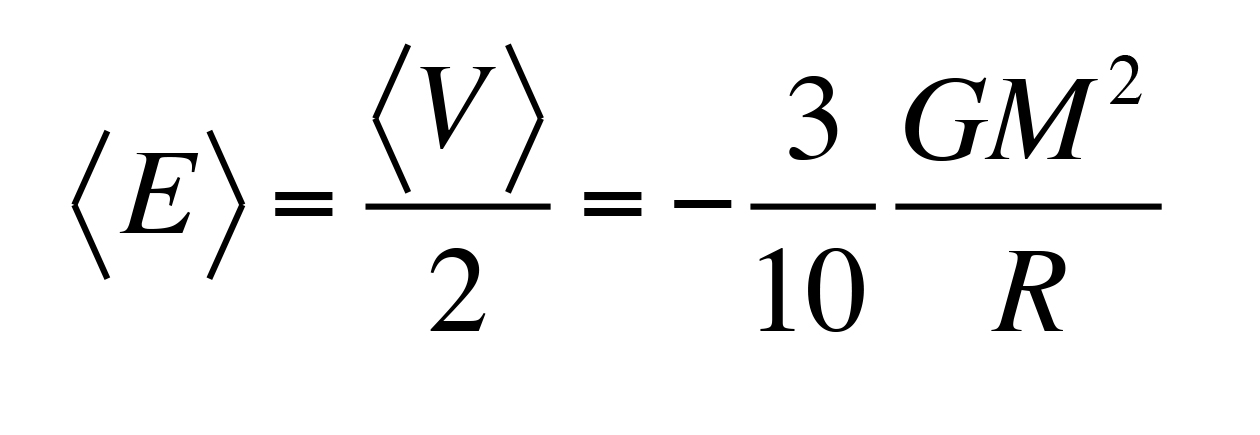
da cui segue che l’energia cinetica media del gas è:
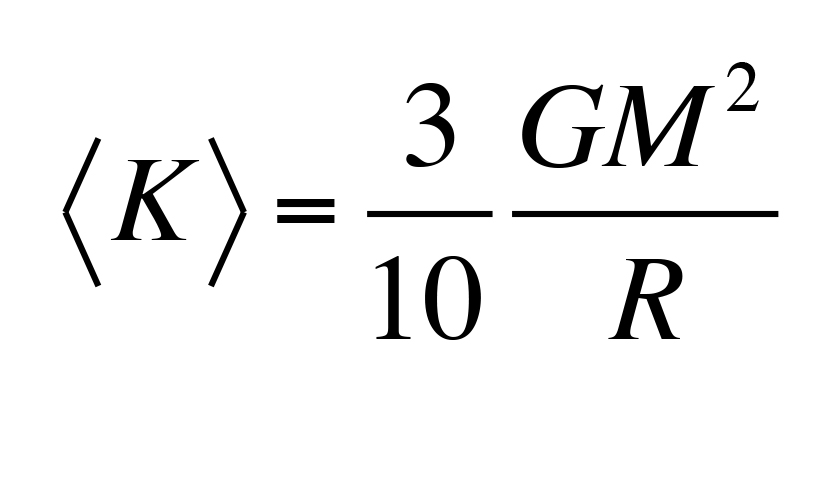
e l’energia disponibile a essere radiata sotto forma di radiazione elettromagnetica è:
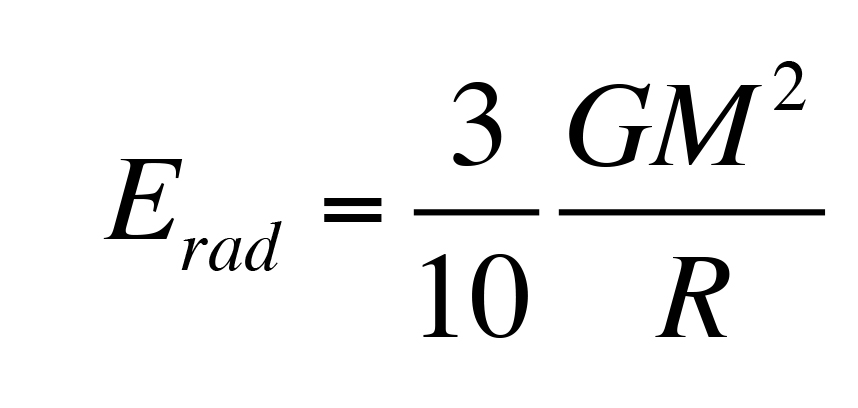
A questo punto, si potrebbe stimare la temperatura della nube utilizzando la teoria cinetica dei gas che lega energia cinetica e temperatura e da quest’ultima e la legge di Stefan-Boltzmann si ottiene la luminosità e dalla teoria del corpo nero si ottiene anche lo spettro della radiazione emessa.
ultimo aggiornamento novembre 2017