Non ho capito cosa c'entra la quantizzazione di Plank con il fatto che a un certo punto, quando viene raggiunta la "massima energia o frequenza" l'onda non si comporta come previsto da Rayleigh-Jeans aumentando la frequenza perché la frequenza non sale più... (un quanto alla volta o di continuo ?) la quantizzazione dell'energia, se ho capito bene, non dovrebbe essere una limitazione all'aumento della frequenza, dice solo che aumenta per quanti e non in continuo all'aumentare dell'energia.
In generale, u(v) può scriversi come u(v)dv=W*dn, ove dn è la densità di modi di oscillazione dell'onda elettromagnetica nell'intervallo [v,v+dv] e W è il valore medio di energia di una radiazione elettromagnetica di frequenza v.
In fisica classica, in base al teorema di equipartizione dell'energia, il corpo nero può essere paragonato ad un gas ideale di temperatura T e dunque W=k*T, ove k è la costante di Boltzmann.
La densità dn può quindi calcolarsi assumendo che, per esempio, il corpo nero sia una cavità cubica e richiedendo che il campo elettromagnetico dia luogo ad onde stazionarie in tale cavità. Così facendo si ottiene:
\[dn=8\pi v^2 dv/c^3\]
ove c è la velocità della luce.
Segue
Segue
\[u(v)dv=8\pi v^2 kT dv/c^3\]
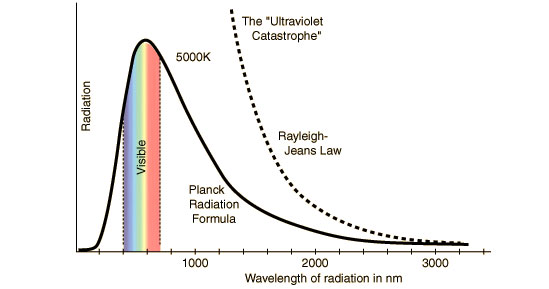
che è la legge di Rayleigh e Jeans che porta alla cosiddetta catastrofe ultravioletta, cioè l'energia della radiazione di un corpo nero tende ad infinito nell'ultravioletto, ovvero all'aumentare della frequenza v.
La catastrofe ultravioletta della legge di Rayleigh e Jeans è stata quindi risolta in meccanica quantistica grazie all'ipotesi di Planck: lo scambio di energia tra materia e radiazione di frequenza v avviene soltanto mediante multipli di un quanto elementare di energia h*v, proporzionale alla frequenza stessa, con h costante di Planck.
Il quanto di energia h*v è il fotone, mediatore delle interazioni elettromagnetiche ed avente spin 1.
Il fotone è quindi un bosone (particella elementare con spin intero) e pertanto deve obbedire alla statistica quantistica di Bose-Einstein, secondo la quale la densità di modi di oscillazione nell'intervallo [v,v+dv] è pari a
La catastrofe ultravioletta della legge di Rayleigh e Jeans è stata quindi risolta in meccanica quantistica grazie all'ipotesi di Planck: lo scambio di energia tra materia e radiazione di frequenza v avviene soltanto mediante multipli di un quanto elementare di energia h*v, proporzionale alla frequenza stessa, con h costante di Planck.
Il quanto di energia h*v è il fotone, mediatore delle interazioni elettromagnetiche ed avente spin 1.
Il fotone è quindi un bosone (particella elementare con spin intero) e pertanto deve obbedire alla statistica quantistica di Bose-Einstein, secondo la quale la densità di modi di oscillazione nell'intervallo [v,v+dv] è pari a
\[dn=8\pi v^2 / (c^3 e^{hv/kT}-1)\]
ove il denominatore
\[1/ (e^{hv/kT}-1)\]
è caratteristico della statistica quantistica bosonica.
Ne segue che, tenendo conto della quantizzazione di Planck, la densità di energia del corpo nero è data da:
Ne segue che, tenendo conto della quantizzazione di Planck, la densità di energia del corpo nero è data da:
\[u(v)dv=hvdn=8\pi v^3/(c^3 e^{hv/kT}-1)\]
È facile mostrare che, grazie alla funzione esponenziale a denominatore, non si ha più la catastrofe ultravioletta, ma la densità di energia tende a zero e non all'infinito nel limite di alta frequenza.
Tornando alla domanda, la quantizzazione di Planck, assieme alla legge statistica di Bose-Einstein, non pone limiti all'aumento di energia o frequenza della radiazione, ma piuttosto ne governa il comportamento nel regime ultravioletto, in modo tale che la densità di energia diminuisca e non aumenti a grandi frequenze.
È interessante notare come per basse frequenze, ossia \(hv \ll kT\) si ha \(e^{hv/kT}-1+hv/(kT)\) e allora si riottiene la legge di Rayleigh e Jeans, come caso particolare dell'equazione di radiazione di Planck.
È facile mostrare che, grazie alla funzione esponenziale a denominatore, non si ha più la catastrofe ultravioletta, ma la densità di energia tende a zero e non all'infinito nel limite di alta frequenza.
Tornando alla domanda, la quantizzazione di Planck, assieme alla legge statistica di Bose-Einstein, non pone limiti all'aumento di energia o frequenza della radiazione, ma piuttosto ne governa il comportamento nel regime ultravioletto, in modo tale che la densità di energia diminuisca e non aumenti a grandi frequenze.
È interessante notare come per basse frequenze, ossia \(hv \ll kT\) si ha \(e^{hv/kT}-1+hv/(kT)\) e allora si riottiene la legge di Rayleigh e Jeans, come caso particolare dell'equazione di radiazione di Planck.
Gennaro Corcella, fisico
ultimo aggiornamento maggio 2019