0132. Che cos'è il secchio di Newton?

 Ho sentito parlare del secchio di Newton che sarebbe connesso alla relatività. Di cosa si tratta? (Erminia Datti)(2009)

Rispondono due dei nostri esperti

1° Risposta

Isaac Newton era un convinto sostenitore dell’esistenza di uno spazio assoluto e per provarne in modo incontrovertibile l'esistenza tentò di individuare un moto assoluto. Egli ritenne di averlo individuato nel famoso esperimento del secchio.

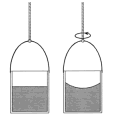
"Se si fa girare su se stesso un vaso appeso ad una corda fino a che la corda, a forza di essere girata, non si possa quasi più piegare, e si mette poi in questo vaso dell'acqua e, dopo aver permesso all'acqua e al vaso di acquistare lo stato di riposo, si lascia che la corda si srotoli. il vaso acquisterà un moto che durerà molto a lungo; all'inizio la superficie dell'acqua contenuta nel vaso resterà piana, come era prima che la corda si srotolasse, ma in seguito, il moto del vaso comunicandosi poco a poco nell'acqua contenuta, quest'acqua comincerà a girare, a elevarsi verso i bordi ed a diventare concava, come ho esperimentato; quindi con l'aumentare del moto il livello dell'acqua crescerà sempre più fino a che, concludendosi le sue rivoluzioni, in tempi uguali ai tempi impiegati dal vaso per fare un giro completo, l'acqua sarà in riposo relativo rispetto al vaso".

Quindi, quando il secchio è in rotazione l'acqua tenderà ad allontanarsi dal centro del secchio e a schiacciarsi lungo le pareti (un pò come in un piccolo gorgo), assumendo la forma detta paraboloide di rotazione, a causa della forza centrifuga. Supponiamo invece che il secchio sia fermo, e che tutto l'universo ruoti attorno a lui. L'acqua nel secchio rimane immobile oppure risente della forza centrifuga? Secondo Newton, dal momento che nessuna forza turba il suo stato di quiete, nessun effetto inerziale muterà la sua forma e nel secchio l'acqua rimarrà ferma come il mare in calma piatta. Le conclusioni di Newton sembrano molto sensate, ma non sono comunemente condivise.

Ernst Mach , ad esempio, sostiene che se il secchio fosse fermo e l'universo tutto girasse attorno ad esso l'acqua assumerebbe ugualmente la forma del paraboloide, come se in realtà stesse ruotando (E. Mach, La meccanica nel suo sviluppo storico-critico, Universale Bollati Boringhieri, Torino, 1992). Per Mach, infatti, l'inerzia non è semplicemente la tendenza di un corpo a rimanere nel suo stato di quiete o di moto rettilineo uniforme, bensì la misura dell'interazione gravitazionale del corpo con tutti gli altri oggetti dell'universo! Conclusioni: Non abbiamo a disposizione due universi, uno con la terra in quiete e un altro con la terra in moto rotatorio, ne abbiamo uno solo, con i suoi moti relativi, i soli che siano misurabili. Non possiamo dire come sarebbero le cose se la terra non girasse, ma solo interpretare in modi diversi l'unico caso che ci è dato. Le leggi della Dinamica possono essere formulate anche in sistemi di riferimento non inerziali e l'esperimento del vaso pieno d'acqua sottoposto a moto rotatorio ci insegna solo che la rotazione relativa dell'acqua rispetto alle pareti del vaso non produce forze centrifughe percettibili, ma che tali forze sono prodotte dal moto rotatorio relativo alla massa della terra e agli altri corpi celesti.

La Teoria della Relatività ha oggi completamente cancellato il concetto di spazio assoluto.

Gaetano Vilasi– Fisico

2° Risposta

Newton ruota un secchio in modo da torcere la corda che lo regge, poi lo riempie d’acqua e lo lascia, dopo il raggiungimento dell’equilibrio del sistema. Il secchio incomincia a girare mentre l’acqua in principio rimane ferma col pelo libero orizzontale. Gradualmente il moto del secchio viene trasferito all’acqua, che pertanto assume una superficie concava. Newton ferma il secchio e l’acqua continua a girare con la sua superficie concava. Come spiegare il comportamento del liquido fermo nel secchio che gira e dell’acqua in rotazione nel recipiente in quiete?

Per eliminare effetti secondari, modifichiamo lievemente la situazione sperimentale, supponendo che il secchio con l’acqua sia al disopra di una piattaforma orizzontale P e il filo sia sostituito da un’asta girevole senza attrito coassiale a P. All’inizio viene fatta ruotare soltanto P, mentre sono fermi il secchio con l’acqua (fig.1). In seguito P viene posta in contatto col secchio che per attrito si mette in rotazione. Quando tutto il sistema consegue la stessa velocità angolare (fig.2), si stacca e si blocca P, mentre l’acqua seguiterà a girare alla stessa maniera (fig.3)

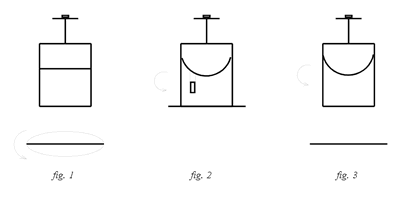Adesso cerchiamo di spiegare questi fenomeni nel riferimento terrestre, in cui sono validi i principi della dinamica per spazi e tempi circoscritti. In fig.1 l’acqua è ferma e ogni goccia, in accordo col principio d’inerzia, è sottoposta al suo peso, alla spinta di Archimede opposta e quindi ad una risultante nulla. In fig.2 e fig.3 i corpuscoli acquosi ruotano uniformemente, perché sono soggetti ad una forza centripeta, provocata dalla concavità della superficie liquida. Infatti, sulla porzione B della goccia agisce una pressione maggiore di quella esplicata sulla parte A, perché B rispetto ad A è situata ad una profondità più grande. La risultante, orientata verso il centro della circonferenza, delle forze orizzontali discordi determina la forza centripeta necessaria per il moto circolare uniforme. Descriviamo il comportamento dell’acqua nel sistema di riferimento della piattaforma. Poiché in fig.3 la P è ferma rispetto alla terra, osserveremo lo stesso moto dai due sistemi di riferimento. In fig.2 e fig.1 la piattaforma rotante, avendo un’accelerazione centripeta, non è più un sistema inerziale in cui sono validi i principi della dinamica. Se vogliamo giustificare il moto nel sistema P, dobbiamo introdurre, oltre alle forze reali cagionate da effettivi agenti fisici, anche delle opportune forze fittizie. In fig.2 notiamo che la superficie dell’acqua è curva, di conseguenza viene esplicata una forza centripeta Fp reale come in precedenza. Poiché le gocce sono pure in quiete devono sottostare ad una forza risultante nulla. Per ottenere questo risultato occorre applicare una forza apparente centrifuga Ff opposta a Fp. Sulla piattaforma in fig.1 vediamo che il secchio e l’acqua hanno una rotazione uniforme opposta a quella di P rilevata dalla terra. Le particelle di acqua sono ferme rispetto alla terra e quindi esposte ad una forza reale nulla. Per comprendere la rotazione uniforme delle stille da P, occorre una forza centripeta da imputare soltanto a sollecitazioni apparenti, indotte dall’accelerazione del sistema di riferimento. Intanto si scorge la presenza di un forza centrifuga, che in questo esempio ha il valore dell’azione centripeta, diretta radialmente verso l’esterno della traiettoria. La situazione impone l’azione di una nuova forza apparente Fc detta di Coriolis con segno discorde e valore doppio di Ff. Così viene prodotta la giusta forza centripeta che giustifica il moto circolare uniforme apparente, visto da P, delle particelle liquide. Quanto precede rappresenta l’interpretazione del moto dell’acqua in due sistemi di riferimento (terra e piattaforma) alla luce della meccanica classica. Newton eseguì l’esperienza del secchio rotante, per introdurre il concetto di spazio assoluto, rispetto al quale riteneva validi i principi della dinamica. Nel sistema di riferimento della piattaforma, riscontriamo che l’acqua è in rotazione sia in fig.1 che in fig.3, ma la superficie dell’acqua è differente essendo prima piana e poi curva. Newton considera il moto dell’acqua dalla piattaforma relativo e non assoluto. In particolare quando P è in quiete rispetto allo spazio assoluto, il moto sarà assoluto anche da P.

Un lungo pendolo, come quello di Foucault , situato a un polo terrestre e posto in oscillazione, conserva l’orientazione del suo piano di vibrazione rispetto ad un sistema inerziale. Dalla terra, che gira intorno al proprio asse, sembra invece ruotare il piano di oscillazione del pendolo. Ernst Mach affermava che il piano del pendolo non ruota rispetto alle stelle fisse. Senza queste, il piano del pendolo dovrebbe rimanere fermo rispetto alla terra. Per Mach sono le stelle fisse che producono le forze apparenti nella rotazione intorno alla terra. Nella concezione di Mach, le forze fittizie e anche l’inerzia di un corpo (tendenza a perseverare nel suo stato di quiete o di moto rettilineo uniforme in assenza di forze) derivano da tutte le masse dell’universo. Queste ipotesi di Mach influenzeranno profondamente le ricerche di Einstein sulla gravitazione. E’ noto che da un sistema inerziale se ne possono trovare infiniti, ossia tutti quelli in moto traslatorio uniforme rispetto al primo. Per esempio, osservando un punto E in moto rettilineo uniforme (mru) da una nave a sua volta in mru rispetto alla terra, ci accorgiamo che E è in mru anche dalla terra. Dunque, il principio d’inerzia funziona sia sulla terra che sulla nave.

Allora non si ha soltanto lo spazio assoluto per l’applicazione dei principi della dinamica, bensì un’infinità di sistemi inerziali in mru fra loro. Einstein estese i sistemi inerziali per la validità, non solo della meccanica, ma di tutte le leggi della fisica. Egli inserì nella teoria (relatività ristretta) la costanza della velocità della luce in tutti i sistemi inerziali, in seguito all’insuccesso di numerosi tentativi, intrapresi da illustri sperimentatori, tesi a rivelare la presenza di uno spazio assoluto, denominato etere, in cui si propagasse la radiazione luminosa. Conseguirono cambiamenti radicali per le definizioni di spazio e tempo, le trasformazioni di coordinate chiamate di Lorentz e le leggi della meccanica. Questi mutamenti tendono a zero, quando la velocità degli oggetti è trascurabile rispetto a quella della luce. Le equazioni di Maxwell dell’elettromagnetismo assumono, invece, la stessa forma allorché si applicano le trasformazioni di Lorentz. Einstein era tormentato dal fatto che i sistemi inerziali fossero dei luoghi privilegiati; egli considerando che le leggi della fisica fossero valide in tutti i sistemi di coordinate, riuscì a formulare la teoria della relatività generale. Einstein partì dal principio di equivalenza tra massa gravitazionale mg (sensibilità dei corpi ai campi gravitazionali) ed inerziale mi (resistenza dei corpi alle accelerazioni). Il peso di un corpo è P = m_g k, dove k è il campo gravitazionale del luogo. Una massa mentre cade, in assenza di resistenza dell’aria, acquista l’accelerazione _g = P / m_i = m_g k / m_i = k, poiché m_g = mi. Risulta che i corpi in caduta libera, a prescindere dalla massa, acquistano la stessa accelerazione pari al campo gravitazionale del posto. Questo fenomeno si può osservare anche in un ascensore privo del campo gravitazionale e dotato di accelerazione g verso l’alto. Nel sistema compaiono delle forze fittizie verso il basso e le masse cadono con la stessa accelerazione g. Si desume che i campi gravitazionali ed apparenti sono equivalenti. Per questo motivo in un sistema in moto spontaneo, è possibile eliminare il campo gravitazionale. In tale riferimento un oggetto soggiace al peso equilibrato dalla forza apparente e rimane fermo se lo era inizialmente. Dalla terra si perviene alla stessa conclusione in quanto l’ascensore e il corpo, fermi nello stesso istante, vengono accelerati identicamente, il che dà luogo alla stessa velocità istantanea e alla quiete della massa relativa al sistema. Un discorso analogo vale per i corpi sospesi nei satelliti artificiali. Bisogna dire che l’eliminazione del campo gravitazionale in un sistema in moto libero non è possibile globalmente ma soltanto localmente (piccoli spazi e brevi tempi). In effetti l’ascensore ha l’accelerazione del suo centro di massa C e quindi un oggetto collocato fermo in C, ivi rimarrà sospeso (fig.4).

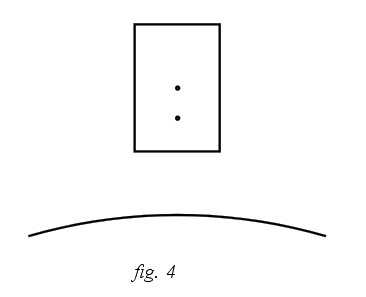Dall’ascensore si può asserire che il campo gravitazionale in C è completamente soppresso dal campo apparente. Una massa ubicata ferma in A si muoverà verso il basso, perché il campo gravitazionale in A supera quello in C, dato che il punto A è più vicino alla terra di C. Poiché il campo gravitazionale in A non viene completamente equilibrato dal campo apparente dell’ascensore, resta in A un campo residuo orientato verso il basso. La non uniformità del campo gravitazionale rende impossibile l’annullamento del campo di gravità in tutti i punti di un sistema in moto libero. Se non vi fossero i campi residui, i diagrammi della quota z in funzione del tempo delle masse in C e A sarebbero delle rette parallele all’asse t (fig.5).

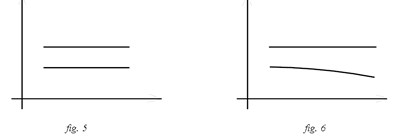È evidente che i residui sono trascurabili in ambiti ristretti di spazio e tempo. In realtà il grafico del punto A, pur avendo la tangente iniziale parallela all’asse t, seguirà una curva non parallela alla retta per C (fig.6).

Per carpire l’essenza di questi diagrammi, consideriamo due punti G e H che partono con direzioni perpendicolari all’asse x in un piano (fig.7) e all’equatore di una sfera (fig.8) e proseguono senza deviazioni laterali rispetto alle superfici. Sul piano i percorsi sono rettilinei e paralleli, sulla sfera le traiettorie intercettano archi di paralleli decrescenti andando verso un polo.

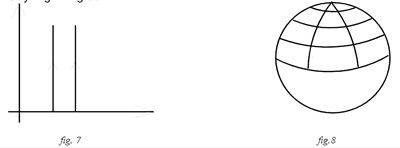Questo ci suggerisce che la prima superficie è piana e la seconda è curva. Alla stessa maniera possiamo arguire che gli effetti gravitazionali residui rendono lo spazio-tempo curvo ed interpretare la gravità come manifestazione di questa curvatura.

Pasquale Catone – Docente di Fisica