 La domanda si riferisce a un caso semplice di un argomento molto vasto che va sotto il nome di clusterizzazione La domanda si riferisce a un caso semplice di un argomento molto vasto che va sotto il nome di clusterizzazione  . .
In questo caso specifico si può procedere ricorrendo al concetto di baricentro che è un caso particolare di clusterizzazione. Prendiamo tre punti su un piano cartesiano di coordinate (x1,y1), (x2,y2), (x3,y3) e di masse m1,m2,m3. Il baricentro (o centro di massa) di coordinate (xcm,ycm) sarà dato dalle formule:
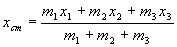
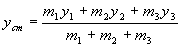
Il punto di coordinate (xcm , ycm) può sostituire, a tutti gli effetti cinematici e dinamici, i tre punti pensandolo con una massa m=m1+m2+ m3. Nel caso particolare della domanda dove si considerano solo i punti e non le masse, nelle formule precedenti basta porre m1=m2=m3=m. Le formule precedenti diventano:
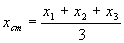
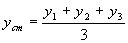
In generale, dati in un piano cartesiano un numero N di punti di coordinate (xi,yi) e di massa mi, il baricentro o centro di massa di coordinate (xcm, ycm) è dato dalle formule:
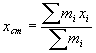 (1) (1)
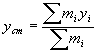
Nel caso specifico della domanda si può considerare che le masse mi siano tutte uguali, allora le formule in (1) si trasformano in:
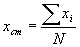
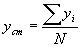
e le coordinate xcm e ycm possono “sostituire” le coordinate dell’insieme dei punti.
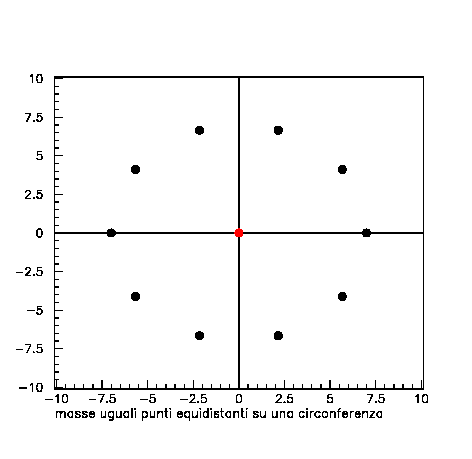
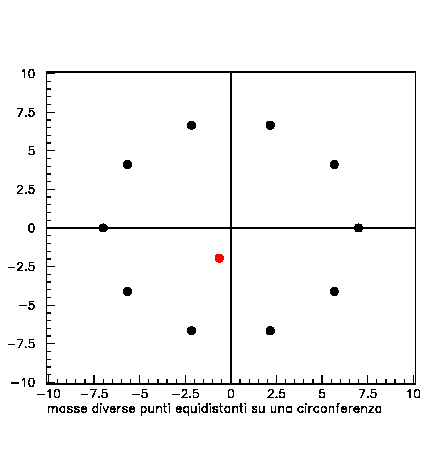
Vediamo con esempi grafici varie configurazioni possibili. Consideriamo punti equidistanti su una circonferenza con masse uguali (baricentro = pallino rosso) e punti equidistanti su una circonferenza con masse non uguali.
Nel primo caso il baricentro coincide ovviamente con il centro del cerchio, essendo tutti i punti simmetrici e di uguale “peso”. Nel secondo caso, pure essendo la distribuzione dei punti simmetrica, il baricentro risulta spostato dal centro proprio per la asimmetria dei “pesi”.
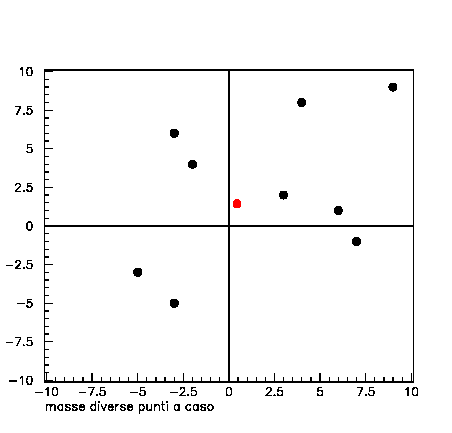
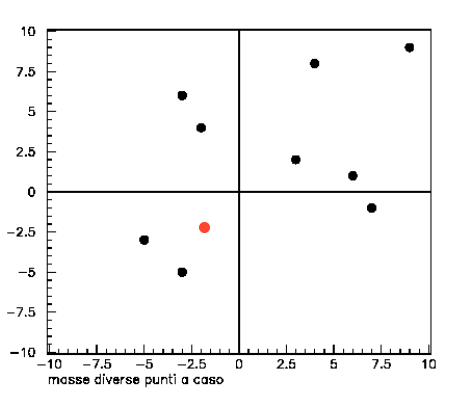
Nella terza e quarta figura sono rappresentate due configurazioni generiche nelle quali i punti sono disposti senza regolarità e i loro “pesi” non sono uguali. Nella seconda delle due sono stati aumentati molto i “pesi” dei due punti nel quadrante inferiore sinistro.
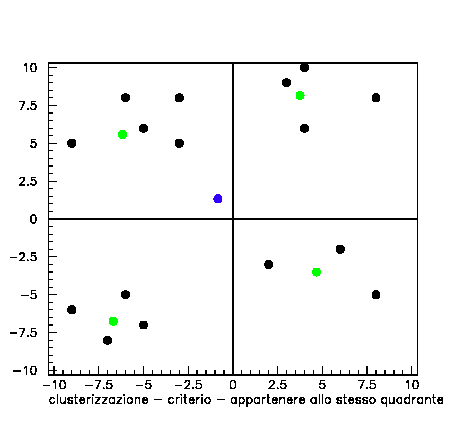
Nell’ ultimo esempio che segue vogliamo far notare che il procedimento di clusterizzazione può essere applicato in vari passi. Immaginiamo di calcolare il baricentro dei punti che si trovano nello stesso quadrante. Nell’esempio le masse sono diverse. Il baricentro di tutti i punti può essere calcolato direttamente (considerando tutti i punti) o sostituendo a ciascun cluster il baricentro parziale, con massa la somma delle masse del cluster considerato, e facendo poi il baricentro dei baricentri parziali. (baricentri parziali = pallino verde, baricentro generale = pallino blu). Il baricentro finale è lo stesso in entrambe le procedure.
 Il problema esposto finora è un caso semplice di problemi molto più generali che si ritrovano nella computer graphics e nei più svariati casi delle analisi statistiche. Le tecniche e gli algoritmi che sono stati elaborati formano una vasta letteratura. Il problema esposto finora è un caso semplice di problemi molto più generali che si ritrovano nella computer graphics e nei più svariati casi delle analisi statistiche. Le tecniche e gli algoritmi che sono stati elaborati formano una vasta letteratura.
Queste tecniche vanno sotto il nome di Cluster Analisys. Con il termine Cluster Analysis si indicano l’insieme delle tecniche di calcolo il cui obiettivo è costituito dall'individuare raggruppamenti di oggetti che abbiano due caratteristiche complementari:
- al loro interno: massima aderenza degli elementi che li compongono al criterio o ai criteri che determinano la loro appartenenza al cluster;
- tra di loro: massima differenza degli elementi che li compongono ai criteri che determinano la loro appartenenza al cluster rispetto agli altri.
In generale, i metodi della Cluster Analysis vengono distinti in due tipi:
- Hierarchical methods, i cui algoritmi ricostruiscono l'intera gerarchia degli oggetti in analisi (il cosiddetto "albero"), vuoi in senso ascendente, vuoi in senso discendente;
- Partitioning methods, i cui algoritmi prevedono che l'utilizzatore abbia preventivamente definito il numero di cluster in cui l'insieme degli oggetti in analisi va diviso.
Massimo Pallotta – Matematico
|


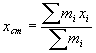
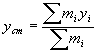
 Il problema esposto finora è un caso semplice di problemi molto più generali che si ritrovano nella computer graphics e nei più svariati casi delle analisi statistiche. Le tecniche e gli algoritmi che sono stati elaborati formano una vasta letteratura.
Il problema esposto finora è un caso semplice di problemi molto più generali che si ritrovano nella computer graphics e nei più svariati casi delle analisi statistiche. Le tecniche e gli algoritmi che sono stati elaborati formano una vasta letteratura.