0140. Che cos'è il momento di una forza?

 Desidererei un chiarimento attorno al concetto di momento di una forza. In alcuni testi di meccanica oltre al momento polare di una forza viene definito un'altro momento (assiale) rispetto non ad un punto ma rispetto ad una retta. Che differenza c'è tra le due cose? Nel piano i due concetti coincidono? (Marcello Lo Iacono)(2026)

Il momento della forza F rispetto al punto O è un vettore con valore uguale al prodotto di F per il braccio b (distanza della forza da O), direzione perpendicolare al piano contenente F ed O, verso fornito dal pollice quando le altre dita della mano destra indicano il senso di rotazione di F attorno a O. Per esempio se F e O appartengono al piano (x,y) di un sistema di assi cartesiani ortogonali come in fig.1, il momento vale M = F b ed è parallelo e concorde all’asse z.

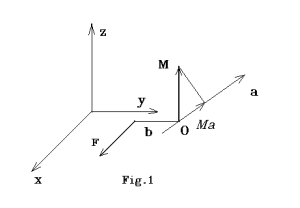
Il momento Ma rispetto ad un asse “a” passante per O è invece uno scalare , rappresentato dal valore della proiezione ortogonale di M nella direzione di "a", preso con segno positivo o negativo secondo che la componente sia concorde o discorde al verso di a (fig.1). Allora i momenti polari e assiali sono concetti diversi, essendo i secondi i valori relativi delle componenti dei primi in una data direzione.

Cominciamo con l’osservare che la forza F si può scomporre in una componente F₂ parallela ad a e in un'altra F₁ giacente in un piano ortogonale ad a (fig.2).

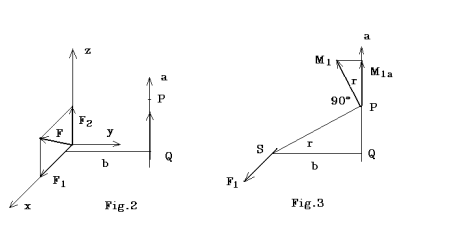
Il momento M₂ di F₂ , rispetto a un qualsiasi punto P di a è sempre perpendicolare ad a. Dunque la proiezione ortogonale di M₂ su a è nulla e cioè la componente assiale di M₂ è sempre zero.

Pertanto per calcolare il momento assiale di F rispetto a P, possiamo sopprimere la componente F2. Il momento di F1 rispetto a P è M1=F₁SP (fig.3), perciò la sua componente nella direzione a ha il modulo M₁ cos r = F₁ SP cos r = F₁ SQ. Questa quantità è l’intensità del momento di F1 rispetto a Q. Se ne conclude che il momento assiale rispetto a qualsiasi punto della retta orientata a assume sempre lo stesso valore. Ecco perché ha senso parlare di momento assiale senza precisare il particolare punto dell’asse. Tale momento equivale allora a Ma = F₁ SQ e ha il segno positivo o negativo se il vettore componente di M nella direzione a è concorde o discorde al verso di a rispettivamente. Se l’asse a è perpendicolare al piano di F e Q, il momento relativo a Q ha la direzione di a e in più questo momento polare ha lo stesso modulo di quello assiale. Però anche in questo caso i due concetti rimangono sostanzialmente diversi, perché il momento polare è un vettore e quello assiale, essendo una sua componente, è uno scalare. Il momento polare è utile quando il corpo è girevole intorno a un polo.

La componente del momento perpendicolare ad a, attorno a cui può ruotare un oggetto rigido, è inefficace trascurando il logoramento dei supporti, perché tende a far girare l’asse che consideriamo fisso. Scaturisce che il momento assiale risulta importante qualora la massa possa ruotare intorno ad un asse fisso.

Pasquale Catone – Docente di Fisica