a cura di Anna Maragno
«Ardano attraverso la notte, lungamente
le stelle lucentissime»1
Il cielo greco (III). Età ellenistica
Ci accostiamo, ora, ai più importanti studi in campo astronomico di età ellenistica: la civiltà greca volge ormai al tramonto. Analizzeremo, in particolare, le intuizioni e le teorie di Aristarco di Samo, di Eratostene di Cirene, di Ipparco di Nicea e di Claudio Tolomeo. Com’è noto, le conclusioni a cui quest’ultimo studioso giunse ebbero un impatto duraturo e rappresentarono, unite alla visione aristotelica dell’universo, il riferimento principale per più di mille anni. Concluderemo, infine, con un rapido sguardo alla celebre macchina di Anticitera.
 Figura 1. Scende la sera sulla loggia delle Cariatidi (lato meridionale dell’Eretteo, tempio ionico del V secolo a.C. situato presso l’Acropoli di Atene).
Figura 1. Scende la sera sulla loggia delle Cariatidi (lato meridionale dell’Eretteo, tempio ionico del V secolo a.C. situato presso l’Acropoli di Atene).
Aristarco di Samo
Aristarco (IV-III secolo a.C.), nato a Samo (isola situata presso la costa della Ionia), studiò ad Alessandria d’Egitto, città da poco fondata da Alessandro Magno che sarebbe presto assurta a centro culturale dell’intero mondo ellenico, sostituendosi all’Atene di età classica.
Aristarco condivise l’ipotesi di Eraclide Pontico secondo la quale la Terra possiede un moto di rotazione attorno al proprio asse della durata di un giorno (di Eraclide Pontico abbiamo parlato nell'articolo Il cielo greco (II). Età classica). Aristarco elaborò, inoltre, una vera e propria teoria eliocentrica secondo la quale il Sole e le stelle fisse rimangono immobili nelle loro posizioni, mentre la Terra ruota attorno al primo. Grazie ad Archimede sappiamo che sorsero dubbi fra alcuni contemporanei, in particolare in merito al moto della Terra attorno al Sole. Più nel dettaglio, gli astronomi si chiedevano come le stelle possano mantenere una posizione fissa durante l’anno se la Terra si trova in costante movimento. Pare, secondo Archimede, che Aristarco replicasse a tali osservazioni affermando che la distanza fra la Terra e le stelle fisse è infinitamente superiore al raggio dell’orbita annuale terrestre e, dunque, non è osservabile alcun effetto di parallasse. L’eliocentrismo di Aristarco conobbe diversi sostenitori. Tra tutti, ricordiamo Seleuco di Seleucia (II secolo a.C.), celebre per i suoi studi sulle maree, basate, secondo il suo pensiero, sull’azione della Luna.
Aristarco si occupò altresì delle dimensioni del Sole e della Luna e delle distanze di questi dalla Terra. Per rispondere a tali quesiti, l’astronomo osservò la Luna nel momento in cui si trova “in quadratura” con il Sole, ossia al primo o all’ultimo quarto. In tali configurazioni, l’angolo centrato sulla Luna che unisce idealmente la Terra, la Luna e il Sole è approssimativamente retto. Con argomenti di tipo trigonometrico, Aristarco concluse che la distanza Terra-Sole è pari a più di 18 volte, ma meno di 20 volte, quella fra la Terra e la Luna (nella realtà, il valore è molto maggiore, ossia circa 390 volte).
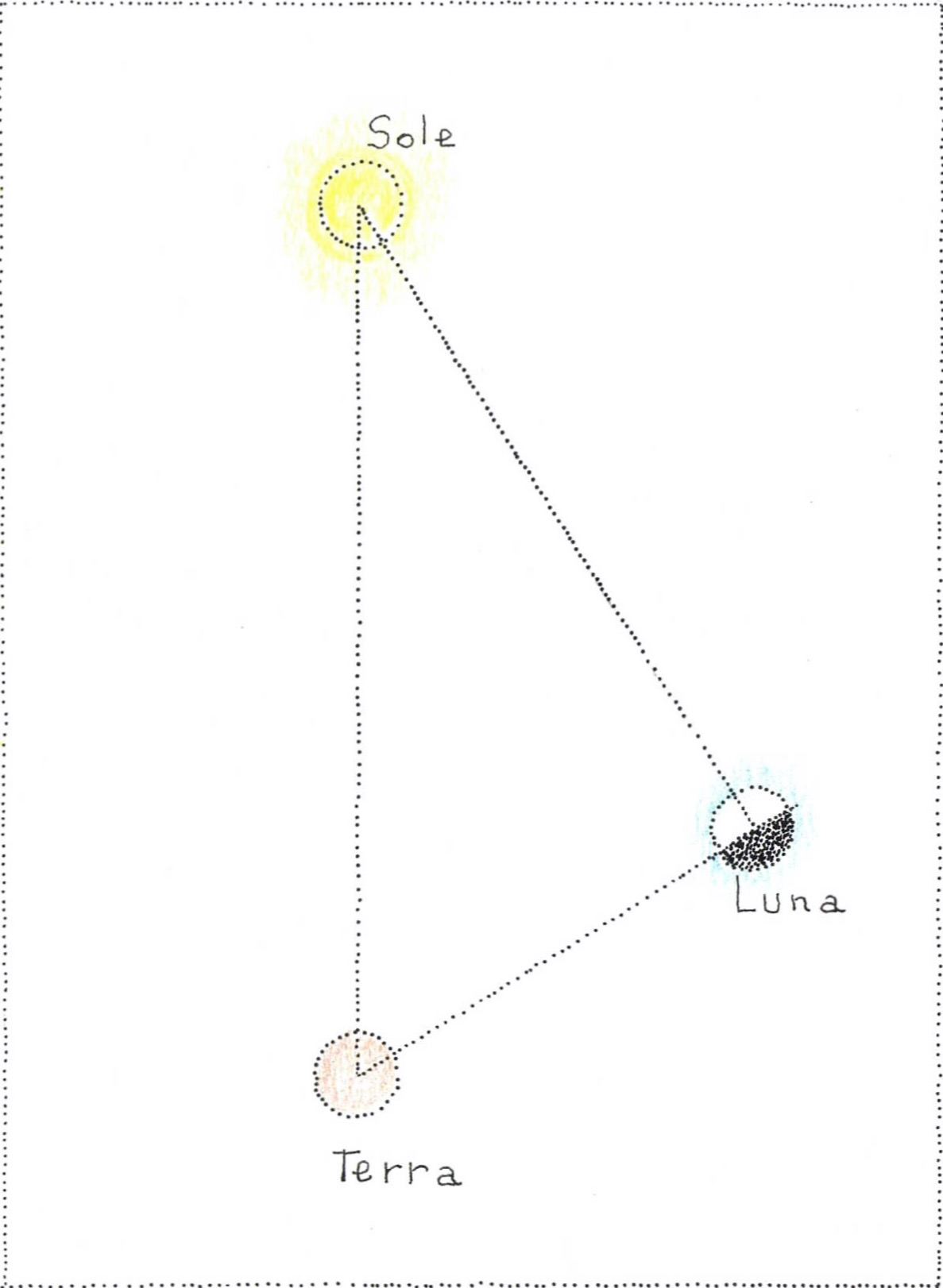
Figura 2. Triangolo rettangolo ai cui vertici sono posti la Terra, il Sole e la Luna in quadratura. Dalla determinazione dell’angolo al cui vertice è posta la Terra, Aristarco fu in grado di stimare la distanza Terra-Sole relativamente a quella Terra-Luna.
Basandosi su tale metodo e sulla durata delle eclissi lunari, Aristarco riuscì a valutare la lunghezza del diametro del Sole, pari a 19 volte quello lunare e a 6 volte quello terrestre (il rapporto reale fra il diametro del Sole e quello della Terra è invece pari a 109). Gli studiosi moderni sono concordi nell’attribuire l’imprecisione dei risultati raggiunti dall’astronomo ad errori di misurazione e, nel contempo, ne riconoscono la correttezza dei ragionamenti teorici. Si sarebbero dovuti infatti attendere i tempi di Giovanni Domenico Cassini (1625-1712) affinché fossero proposti sistemi più performanti per la determinazione delle distanze della Luna e del Sole dalla Terra.
Secondo la testimonianza di Vitruvio, pare, inoltre, che Aristarco avesse realizzato anche un interessante strumento consistente in quadrante solare emisferico.
Eratostene di Cirene
Matematico, astronomo e geografo, così come filologo, geografo, grammatico e filosofo, Eratostene nacque a Cirene (nell’attuale Libia, tra il III e il II secolo a.C.); visse ad Atene e successivamente ad Alessandria d’Egitto, dove diresse per qualche tempo la celebre Biblioteca. Diversi furono i suoi contributi nel campo dell’astronomia, ma è universalmente noto per il così detto “Metodo di Eratostene”. Tale metodo consiste nella più accurata determinazione della circonferenza terrestre in età antica compiuta con l’ausilio di un unico, semplice strumento: lo gnomone (ossia un asse collocato verticalmente su un piano a questo perpendicolare). Eratostene suppose innanzitutto che le città di Alessandria e di Siene si trovassero sullo stesso meridiano. Lo studioso notò poi che, a mezzogiorno del solstizio d’estate, il Sole si trovava allo zenit nella città di Siene: ivi, infatti, illuminava il fondo dei pozzi e, dunque, si trovava sulla verticale del luogo. Ciò non accadeva ad Alessandria, situata più a settentrione, dove lo gnomone proiettava un’ombra sul terreno con un angolo pari a 7,2° (ossia 1/50 dell’angolo giro). Da tale misurazione Eratostene dedusse che la circonferenza della Terra dovesse misurare 50 volte la distanza tra Siene ed Alessandria. Dato che quest’ultima era pari a circa 5.000 stadi, la circonferenza terrestre doveva allora misurare 250.000 stadi (corrispondenti a 46.212 km o a 44.400 km, a seconda che l’astronomo si riferisse allo “stadio alessandrino” o a quello “attico”). Si tratta, in entrambi i casi, di un valore estremamente vicino a quello calcolato con mezzi odierni, pari a 40.075 km.
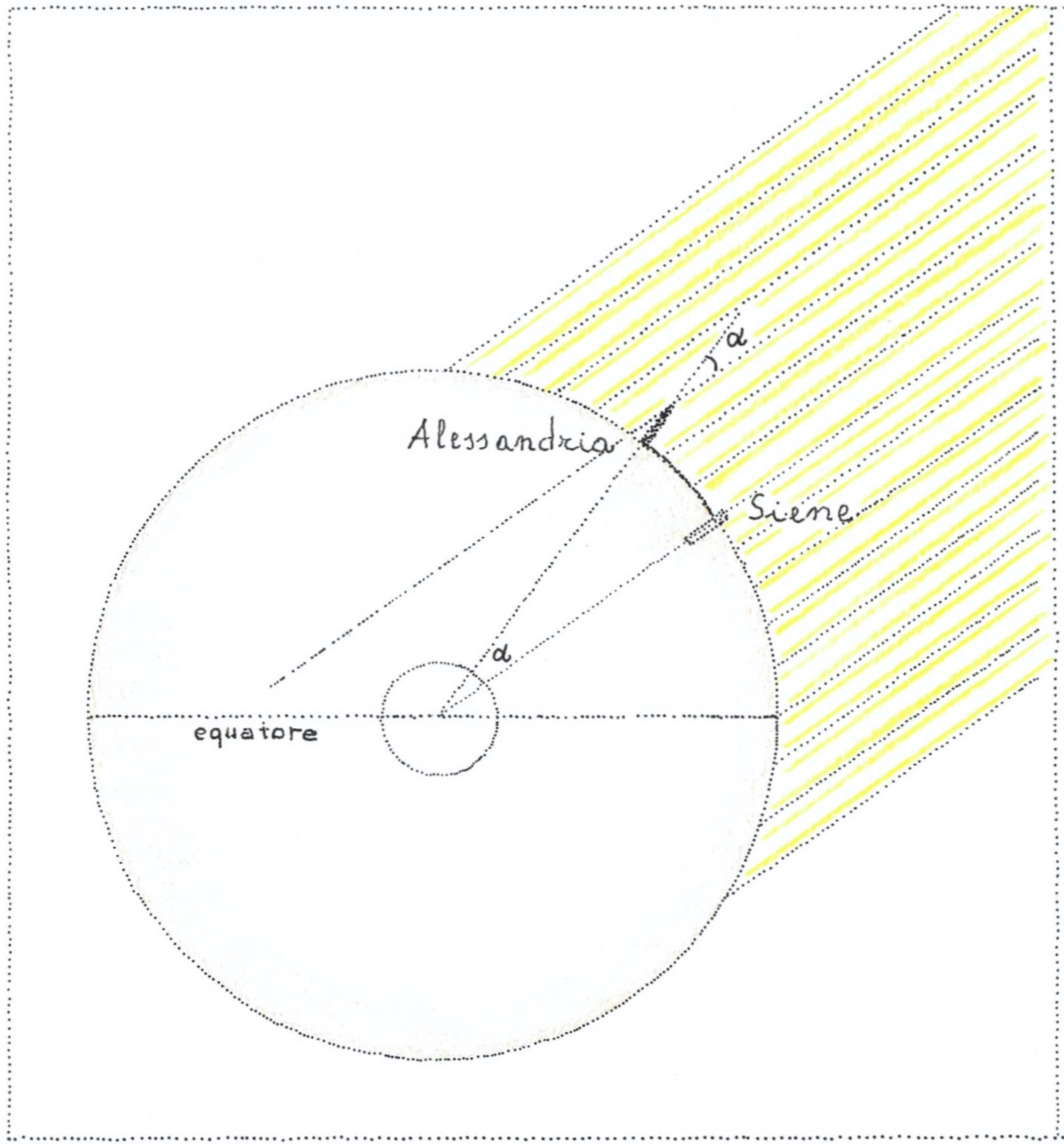
Figura 3. Un possibile schema del ragionamento di Eratostene: il rapporto tra la circonferenza della Terra e la distanza fra Siene ed Alessandria è posto in relazione con quello tra l’angolo giro (360°) e l’angolo α.
In conclusione, Eratostene giunse ad una misurazione molto precisa; non possiamo dire lo stesso per quelle di Aristarco. Ciò che rende di straordinario valore i tentativi di entrambi gli scienziati non furono tanto i risultati ai quali pervennero (nel caso di Aristarco, macchiati da errori dovuti all’insufficienza della strumentazione disponibile all’epoca), quanto al rigore dei loro metodi e dei loro modelli.
Ipparco di Nicea
Ipparco (II secolo a.C.), nato a Nicea (nella Bitinia), trascorse la maggior parte della propria vita a Rodi, dove svolse osservazioni astronomiche per oltre trent’anni. È riconosciuto da molti studiosi come il più grande astronomo del mondo classico. Stilò un preciso catalogo (oggi perduto) di circa 850 stelle, ordinate secondo 6 classi di luminosità, grazie all’introduzione della scala della magnitudine apparente. In base a questa, le stelle di prima magnitudine sono le più luminose nel cielo, quelle di seconda magnitudine brillano la metà delle prime e così di seguito fino alla sesta magnitudine, corrispondente alle stelle la cui osservazione si pone al limite della visione umana, senza l’ausilio di strumentazione, in una notte serena senza Luna.

Figura 4. Ipparco osserva il cielo stellato presso l’Osservatorio di Alessandria d’Egitto. Libera interpretazione dell’illustrazione dal titolo Hipparcus in the Observatory of Alexandria, contenuta nel volume The Story of the Sun, Moon, and Stars (1879) di Agnes Giberne.
Ipparco, confrontando le coordinate stellari da lui registrate con quelle che gli astronomi Aristillo e Timocari avevano fornito circa 150 anni prima del suo tempo, intuì inoltre il fenomeno della precessione degli equinozi. Altre sue ricerche in campo astronomico lo portarono ad ideare un efficace metodo per prevedere le eclissi solari e lunari. Stimò altresì le dimensioni della Luna e del Sole e le loro distanze dalla Terra e osservò una nova nella costellazione dello Scorpione. Molti esperti attribuiscono ad Ipparco le invenzioni dell’astrolabio e della sfera armillare, strumenti che potrebbe aver utilizzato per compilare il proprio catalogo stellare. Oltre all’astronomia, si interessò anche alla meteorologia, alla matematica e all’ottica: fondamentale è, ad esempio, il suo contributo allo sviluppo della trigonometria.

Figura 5. La costellazione Il Cavallino, posta a sinistra della testa di Pegaso. Verosimilmente identificata da Ipparco, fu poi inserita da Tolomeo nel suo catalogo di 48 costellazioni. Libera interpretazione della Tavola X dell’Uranographia di Johann Bode (1801).
Claudio Tolomeo
Astronomo, matematico e geografo, Claudio Tolomeo (II secolo d.C.) è conosciuto principalmente per il suo trattato astronomico divenuto noto come Almagesto (titolo originale: Μαϑηματικὴ σύνταξις), in cui si trova esposto l’intero sistema astronomico da lui elaborato, fondato – in gran parte – sulle osservazioni di Ipparco. I tredici libri di cui è composto trattano diversi argomenti, quali la trigonometria sferica, i moti del Sole e della Luna, la distanza di questi dalla Terra, le eclissi, un catalogo di stelle (di cui parleremo tra poco) e la teoria dei pianeti. Secondo Tolomeo la Terra, di forma sferica, è immobile al centro della sfera delle stelle fisse; attorno alla prima ruotano il Sole, la Luna e i pianeti allora conosciuti (Mercurio, Venere, Marte, Giove, Saturno). Per spiegare le irregolarità osservative connesse ai loro moti, Tolomeo introduce complessi modelli basati sulla composizione di più moti circolari uniformi e basati su deferenti, epicicli ed eccentrici. Alcuni di questi schemi teorici erano stati già proposti da Apollonio di Perga (approssimativamente nel 200 a.C.) e probabilmente utilizzati da Ipparco; Tolomeo li modificò, completandoli e rendendoli in grado di descrivere anche i moti retrogradi dei pianeti.
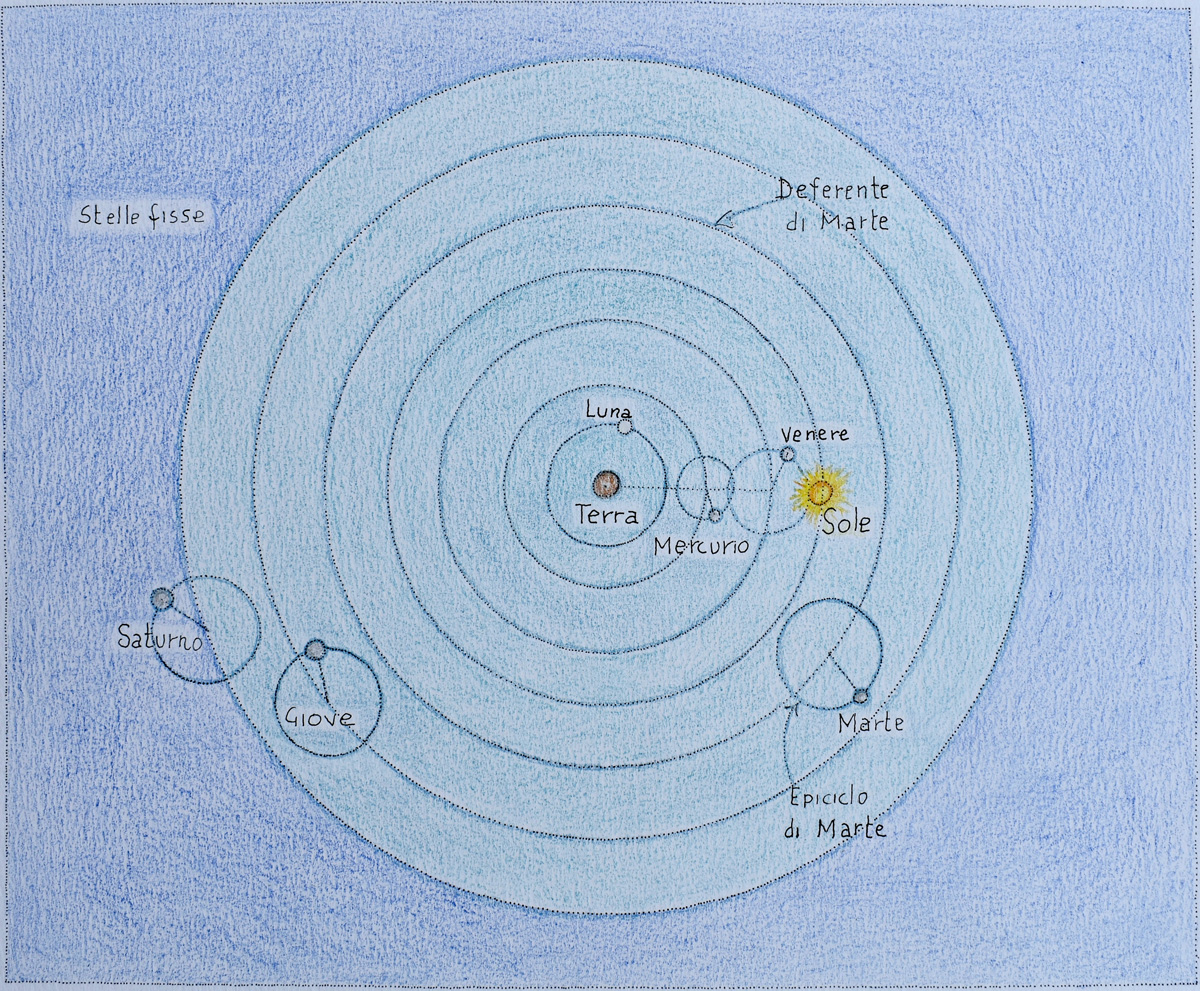
Figura 6. Visione tolemaica del Sistema Solare. A ciascun pianeta sono associati due moti circolari simultanei, di cui uno attorno alla Terra.
L’Almagesto contiene, come anticipato, un catalogo stellare di 1.022 stelle e 48 costellazioni (includendo altresì le nebulose) visibili ad Alessandria d’Egitto, in gran parte basato su quello precedente di Ipparco. Il catalogo di Tolomeo rappresenta il più accurato elenco stellare dell’antichità classica e costituì un riferimento imprescindibile per l’astronomia fino al XVII secolo.
In un’altra opera, dal titolo Ipotesi planetarie (Ὑποθέσεις τῶν πλανωμένων), Tolomeo tratta argomenti quali la struttura dell’universo e le leggi che governano i moti dei corpi celesti. L’astronomo descrive un sistema planetario formato da otto sfere celesti concentriche: una per il Sole, una per la Luna, cinque per i pianeti e una per le stelle fisse (fornendo, sul punto, spiegazioni più precise rispetto a ciò che si trova esposto nell’Almagesto). Vi si trovano, altresì, stimate le distanze della Luna, del Sole e delle stelle fisse dalla Terra e i raggi dei primi due, ponendo come unità di misura il raggio terrestre (secondo l’astronomo, di lunghezza pari a 8.500 km). Dai suoi calcoli, la Terra disterebbe 59 raggi terrestri dalla Luna (ossia 480.000 km, mentre il valore reale è pari a 384.500 km) e 1.210 raggi terrestri dal Sole (ossia 8 milioni di km dal Sole, mentre nella realtà è lontana 149 milioni di km). Infine, la sfera delle stelle fisse, la più lontana dalla Terra, disterebbe 20.000 raggi terrestri dal nostro pianeta (ossia 160 milioni di km) e tale valore coinciderebbe dunque con il raggio dell’universo quantificato da Tolomeo. L’astronomo calcola anche i raggi della Luna e del Sole in rapporto a quello terrestre: se questo è pari a 1, quello della Luna è ¼, quello del Sole 5.
Le opere di Tolomeo, come già abbiamo anticipato, esercitarono un’influenza capitale sull’astronomia dei secoli successivi. La visione tolemaica dell’universo, nonostante alcuni punti di scostamento, fu fusa dalla tradizione con quella aristotelica: il risultato fu la composizione di un modello che dominò l’intera interpretazione del cosmo per oltre un millennio, fino alla prima età moderna e alla rivoluzione copernicana.

Figura 7. Urania, musa dell’astronomia, guida Claudio Tolomeo allo studio del cielo. Libera interpretazione di una xilografia contenuta nell’opera Margarita Philosophica di Gregor Reisch (1503).
La macchina di Anticitera, un tesoro di età ellenistica
Concludiamo la nostra concisa trattazione dell’astronomia ellenistica soffermandoci brevemente sul meccanismo di Anticitera, rinvenuto più di un secolo fa nel relitto di una nave mercantile romana naufragata nel I secolo a.C. al largo dell’omonima isola (posta tra Creta e il Peloponneso). La macchina, realizzata in rame, misurava 30 cm in lunghezza, 20 cm in larghezza e 10 cm di spessore ed era stata collocata in una cornice lignea all’interno della nave. Gli ingranaggi consistevano in un insieme di ruote dentate, azionate a mano, sulle quali era riportato un fitto numero di iscrizioni. Nei decenni successivi alla scoperta, furono condotte numerose ricerche al fine di dipanare il mistero relativo al suo funzionamento: secondo gli studi più recenti, il meccanismo era uno strumento astronomico in grado di predire i moti della Luna, del Sole e dei pianeti e le eclissi. Pare che il dispositivo costituisse, inoltre, una sorta di “calcolatore” che fungeva da calendario solare e lunare. Molti altri aspetti riguardanti questa singolare macchina rimangono, ad oggi, ancora celati.

Figura 8. Il frammento A (il più grande) della macchina di Anticitera, oggi conservato presso il Museo Nazionale di Archeologia di Atene.
Testi e disegni originali di Anna Maragno. Non riprodurre senza autorizzazione.
Note
1. Ibico, Lo stellato, in Lirici greci tradotti da Salvatore Quasimodo, Arnoldo Mondadori Editore, Milano, 1951, p. 83.
Fonti delle immagini
Figura 1. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.
Figura 2. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.
Figura 3. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.
Figura 4. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.
Figura 5. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.
Figura 6. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.
Figura 7. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.
Figura 8. No machine-readable author provided. Marsyas assumed (based on copyright claims)., licenza Creative Commons CC BY-SA 3.0 <http://creativecommons.org/licenses/by-sa/3.0/>, via Wikimedia Commons al link:
https://commons.wikimedia.org/wiki/File:NAMA_Machine_d%27Anticyth%C3%A8re_1.jpg
Bibliografia e consigli di lettura
Bersanelli, M., Il grande spettacolo del cielo. Otto visioni dell’universo dall’antichità ai nostri giorni, Sperling & Kupfer, Milano, 2018
Boitani, P., Il grande racconto delle stelle, Società editrice il Mulino, Bologna, 2012
Bowen, A. C., Goldstein, B. R., Hipparchus’ Treatment of Early Greek Astronomy. The Case of Eudoxus and the Length of Daytime, 135, fasc. 2 (1991), pp. 233-254
Brooke-Hitching, E., L’Atlante del Cielo. Le mappe più belle, i miti e le meraviglie dell’universo, tr. it. a cura di V. Gorla, Mondadori, Milano, 2020
Dutka, J., Erathostenes’ Measurement of the Earth Reconsidered, in «Archive for History of Exact Sciences» 46, fasc. 1 (1993), pp. 55-66
Efstathiou, K., Efstathiou, M., Basiakoulis, A., Kokkinos, N., The Antikythera Mechanism: The Prove of the Accuracy of the Astronomical Calculations Based on It, in «Heritage» 4, fasc. 4 (2021), pp. 3848-3878
Fischer, I., Another look at Erathostenes’ and Posidonius’ Determinations of the Earth’s Circumference, in «Quarterly Journal of the Royal Astronomical Society» 16 (1975), pp. 152-167
Fowler, D. H., Erathostenes on the “Measurement” of the Earth, in «Historia Mathematica» 11 (1984), pp. 411-416
Freeth, T., Higgon, D., Dacanalis, A., MacDonald, L., Georgakopoulou, M., Wojcik, A., A Model of the Cosmos in the ancient Greek Antikythera Mechanism, in «Scientific Reports» 11, pp. 1-15
Graßhoff, G., The History of Ptolemy’s Star Catalogue, Springer-Verlag, New York, 1990
Gulbekian, E., The Origin and Value of the Stadion Unit Used by Erathostenes in the Third Century B.C., in «Archive for History of Exact Sciences» 37, fasc. 4 (1987), pp. 359-363
Hack, M., Ferreri, W., Cossard, G., Il lungo racconto dell’origine. I grandi miti e le teorie con cui l’umanità ha spiegato l’Universo, Sperling & Kupfer, Milano, 2018
Heath, T. L., Aristarchus of Samos, the ancient Copernicus. A history of Greek Astronomy to Aristarchus, Together with Aristarchus’s Treatise on the Sizes and Distances of the Sun and Moon, Claredon Press, Oxford, 1913
Leopardi, G., Storia dell’astronomia dalla sua origine fino all’anno MDCCCXIII, con uno scritto di A. Massarenti e un’appendice di L. Zampieri, BookTime, Milano, 2008
Murschel, A., The Structure and Function of Ptolemy’s Physical Hypotheses of Planetary Motion, in «Journal for the History of Astronomy» 26, fasc. 1 (1995), pp. 33-61
Pichot, A., La nascita della scienza. Mesopotamia, Egitto, Grecia antica, tr. it. a cura di M. Bianchi, Edizioni Dedalo, Bari, 1993
Russo, L., The astronomy of Hipparchus and his time: a study based on pre-ptolemaic sources, in «Vistas in Astronomy» 38 (1994), pp. 207-248
Sciarma, C., Il meccanismo di Antikythera, pubblicato online il 29/07/2022 in «Media INAF. Il notiziario online dell’Istituto nazionale di astrofisica», consultabile al link: https://www.media.inaf.it/2022/07/29/il-meccanismo-di-antikythera/#:~:text=Il%20Meccanismo%20di%20Antikythera%20era,%2C%20Marte%2C%20Giove%20e%20Saturno
Seiradakis, J. H., Edmunds, M. G., Our current knowledge of the Antikythera Mechanism, in «Nature Astronomy» 2 (2018), pp. 35-42
Swerdlow, N. M., The Enigma of Ptolemy’s Catalogue of Stars, in «Journal for the History of Astronomy» 23, fasc. 3 (1992), pp. 173-183
Toomer, G. J., Hipparchus on the Distanced of the Sun and Moon, in «Archive for History of Exact Sciences» 14, fasc. 2 (1974), pp. 126-142
Voulgaris, A., Mouratidis, C., Vossinakis, A., Bokovos, G., Renumbering of the Antikythera Mechanism Saros cells, resulting from the Saros spiral mechanical apokatastasis, in «Mediterranean Archaeology and Archaeometry» 21, fasc. 2 (2021), pp. 107-128

