Il cielo greco (II). Età classica

a cura di Anna Maragno

«Era tutto un ricamo trapunto»¹

Il cielo greco (II). Età classica

Dopo aver descritto il cielo greco arcaico, proseguiamo il nostro viaggio nell’astronomia e nella cosmologia fiorite in età classica. Queste discipline, già indagate dagli appartenenti alla scuola pitagorica, furono in seguito approfondite da filosofi e studiosi quali Parmenide e Anassagora. Giungeremo alle lucide trattazioni di Platone, di Eudosso di Cnido, di Callippo di Cizico e di Aristotele, accennando, infine, agli studi di Eraclide Pontico. Alcune delle intuizioni di cui avremo modo di parlare ebbero ripercussioni importanti, in particolare perché posero le basi a concetti propri della scienza e dell’astronomia moderne. 

Figura 1. Libera interpretazione de L’Accademia di Platone, mosaico policromo di 86 cm x 85 cm, proveniente dalla villa di Titus Siminius Stephanus a Pompei e oggi conservato presso il Museo Archeologico Nazionale di Napoli. Fra le sette figure rappresentate, gli esperti concordano nell’individuare Platone come il terzo filosofo da sinistra, che indica il globo con un bastoncino di legno. Non esiste accordo, però, sugli altri filosofi ritratti: sono stati proposti diversi nomi, quali Talete, Anassagora, Pitagora, Democrito, Eudosso, Callippo, Metone, Ipparco e Arato. Alcuni studiosi identificano gli uomini rappresentati con i Sette Savi. Dietro di loro, a destra, sono visibili le mura di Atene (o, secondo altri, l’Acropoli); al centro della figura, una colonna è sormontata da una meridiana.

La scuola pitagorica 

Pitagora (571-570 a.C. - 497-496 a.C.), nato a Samo (nella Ionia), condusse probabilmente numerosi viaggi nel mondo allora conosciuto prima di stabilirsi a Crotone, nella Magna Grecia, dove fondò la propria scuola. Questa era una sorta di comunità mistico-religiosa che imponeva ai seguaci numerose regole e divieti. Pitagora era ritenuto depositario di sapienza divina e, dunque, la sua dottrina era accettata senza possibilità di discussione (come recita il celebre αὐτὸς ἔφα, ipse dixit)². Tra le discipline studiate dai Pitagorici spiccava la musica: essi scoprirono i rapporti numerici tra le diverse altezze (e quindi le frequenze) delle note musicali. Furono forse queste indagini a far sorgere il loro profondo interesse verso la matematica, considerata una vera e propria scienza. Nel pensiero pitagorico, l’ἀρχή non è rappresentato dall’acqua (come per Talete), né dall’ἄπειρον (di Anassimandro) né dall’aria (secondo quanto riteneva Anassimene), bensì dal “numero”: dunque, tutte le cose sarebbero composte da numeri, secondo un ordine geometrico misurabile. Attraverso i numeri sarebbe quindi possibile offrire una spiegazione ad ogni fenomeno naturale, anche astronomico. I Pitagorici erano convinti che i corpi celesti, tra cui la Terra, presentassero una forma sferica. La sfera, infatti, era considerata la forma geometrica perfetta, concepita come immagine dell’armonia poiché tutti i punti di cui è costituita sono equidistanti dal centro. 

Dopo Pitagora, seguaci della sua scuola formularono teorie astronomiche contenenti intuizioni sorprendenti. Si deve ricordare innanzitutto Filolao (470 a.C. - 390 a.C.), additato dagli studiosi come un possibile precursore dello stesso Copernico, in quanto avverso al geocentrismo. Il filosofo affermava, infatti, che la Terra non si trova in una posizione fissa al centro dell’universo ma, come gli altri corpi celesti, ruota attorno ad un fuoco centrale (chiamato Hestia) dal quale ha origine tutta la materia. Il movimento dei corpi celesti (che, per Filolao, sono in numero di dieci) attorno a Hestia procede da oriente ad occidente e coinvolge, dall’esterno verso l’interno, il cielo delle stelle fisse (il più lontano dal centro), i cinque pianeti (Saturno, Giove, Marte, Mercurio, Venere), il Sole (che riflette i raggi luminosi del fuoco centrale), la Luna, la Terra e, infine, l’Antiterra (un pianeta di cui il filosofo suppone l’esistenza per raggiungere il sacro numero di dieci). 

Un altro discepolo della scuola, Ecfanto di Siracusa (IV secolo a.C.), sarebbe stato il primo ad ipotizzare che la Terra, posta al centro dell’universo, ruoti attorno al proprio asse da ovest verso est.

Figura 2. Fyodor Andreyevich Bronnikov (1827-1902), I pitagorici celebrano il sorgere del sole, olio su tela, 1869, 99,7 cm x 161 cm, Galleria Tret’jakov, Mosca, Russia.

Parmenide e Anassagora

Secondo alcuni studiosi, a Parmenide di Elea (VI-V secolo a.C.) erano noti sia la sfericità della Terra e della Luna, sia la natura delle fasi lunari (dovute alle reciproche posizioni dei due corpi). Per il filosofo, inoltre, la Luna non brilla di luce propria, bensì riflette quella che riceve dal Sole. Infine, pare che il filosofo avesse ipotizzato un’origine del Sole e della Luna dalla via Lattea: il primo staccandosi dalla zona più calda e rada, la seconda da quella più densa e fredda. 

Anche Anassagora (499 a.C. - 428 a.C.), amico e maestro di Pericle, si interessò allo studio del cielo; le sue teorie furono tanto rivoluzionarie per l’epoca da costargli l’esilio da Atene. Alcuni avversari politici di Pericle, infatti, allo scopo di allontanare il filosofo da quest’ultimo, accusarono Anassagora di empietà, in quanto, nella sua opinione, il Sole era null’altro che una massa di metallo incandescente riscaldato dal moto nell’etere e la Luna una sfera rocciosa. Dunque, nel suo pensiero, i due corpi non erano associati ad alcuna divinità. Il filosofo cercò inoltre di dare risposta a molti altri quesiti concernenti la volta celeste. Eseguì una stima delle dimensioni del Sole, secondo la quale l’astro è poco più grande del Peloponneso e spiegò l’origine delle eclissi di Sole e di Luna. Come accennavamo, egli credeva che quest’ultima fosse un corpo opaco che riflette la luce del Sole e sulla cui superficie sono presenti montagne e valli; ancora, egli giunse a supporre che potesse essere abitata. Anassagora affermò poi che i meteoriti sono frammenti rocciosi di corpi celesti e fu in grado di prevedere la caduta di uno di questi nei pressi del fiume Egospotami nel secondo anno della 78° Olimpiade (467 a.C.). Il filosofo espresse, infine, la convinzione che la Terra fosse piatta e che le stelle fossero masse rocciose staccatesi dal nostro pianeta e rese infuocate a causa della loro rapida rotazione. 

Il grande interesse di Anassagora nei confronti dell’astronomia è nitidamente espresso nel suo epitaffio. Lo riporta Diogene Laerzio: «Qui giace Anassagora che moltissimo s’accostò /Al limite della verità intorno al mondo celeste» (Diogene Laerzio, De clarorum philosophorum vitis, II, 6, 15). 

Platone

In questa sede non possiamo trattare approfonditamente la visione cosmologica di Platone (428-427 a.C. - 348-347 a.C.) e dovremo necessariamente limitarci a offrire soltanto alcuni cenni. Più in particolare, focalizzeremo la nostra attenzione sul Dialogo Timeo, non mancando però di dare conto delle sue più significative affermazioni in ambito astronomico ricavabili in altri suoi scritti. Ebbene, nel Timeo sono trattati, principalmente, l’origine dell’universo, la struttura di quest’ultimo e, infine, la natura umana. Concentriamoci brevemente sui primi due argomenti. Secondo Platone, il cosmo, di forma sferica, ha avuto origine dall’azione di un Demiurgo che lo avrebbe plasmato a partire dai quattro elementi (terra, acqua, aria e fuoco), ordinandoli sulla base di quattro solidi geometrici (e, dunque, su numeri). Infatti, per Platone, alla terra è associato il cubo, all’acqua l’icosaedro, al fuoco il tetraedro e all’aria l’ottaedro. Successivamente, il Demiurgo avrebbe creato il tempo e i corpi celesti. La struttura dei cieli, secondo il filosofo, poggia su due circoli: il circolo del medesimo, ossia l’equatore celeste, e il circolo del diverso, ossia l’eclittica. I due condividono il medesimo centro fisso, ossia la Terra, di forma sferica. Il circolo del medesimo, muovendosi uniformemente da est ad ovest, governa la rivoluzione diurna della volta celeste; il circolo del diverso, che si muove in senso opposto, è suddiviso in sette cerchi concentrici corrispondenti ai diversi pianeti, i quali ruotano a velocità differenti a seconda della rispettiva distanza dal centro. Dal più vicino al più lontano, troviamo quindi la Luna, Mercurio, Venere, il Sole, Marte, Giove e Saturno (Figura 3). 

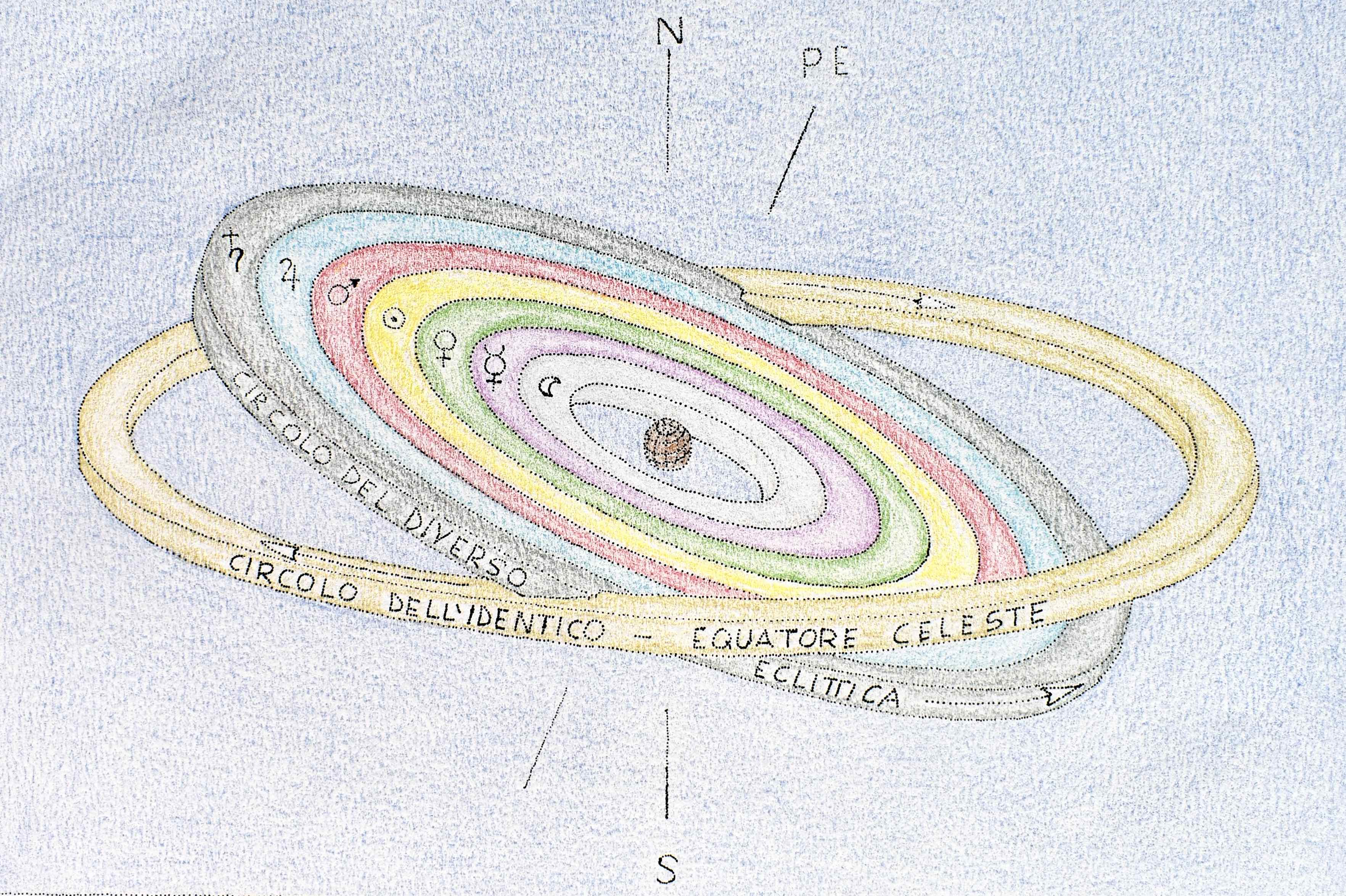
Figura 3. La struttura del cosmo secondo Platone. Sono visibili, oltre al circolo dell’identico e a quello del diverso, anche l’asse del mondo (NS) e il polo dell’eclittica (PE).

Lasciamo ora Platone per descrivere il pensiero di un discepolo della sua scuola (la celebre Accademia, fondata nel 387 a.C.): Eudosso di Cnido (408 a.C. - 355 a.C.).

Eudosso di Cnido

Dopo aver compiuto i propri studi ad Atene, Eudosso intraprese un viaggio in Egitto, in occasione del quale ebbe modo di accostarsi alle ricerche e alle osservazioni astronomiche condotte dai sacerdoti di Eliopoli. Tornato in patria arricchito di tali conoscenze, approfondì, oltre all’astronomia, numerosi aspetti delle discipline della geometria, della matematica, della teoria delle macchine e lo studio dell’armonia. In aggiunta, egli brillava nella scienza oratoria. Per quanto concerne più specificamente l’astronomia, si deve ad Eudosso la prima compiuta elaborazione di un modello planetario basato su calcoli matematici. La sua teoria, che mostra profili di elevata complessità, è legata alle cosiddette “sfere omocentriche”, ossia aventi un unico centro di rotazione in corrispondenza del quale è posizionata la Terra, immobile. Attorno a questa si muovono le sfere con moto circolare uniforme, ciascuna ad una diversa velocità a seconda della rispettiva distanza dal centro. Ad alcune di queste sfere sono associati i pianeti e alla più esterna le stelle fisse. La composizione di questi movimenti era in grado di spiegare, con buona approssimazione, i moti apparenti dei corpi celesti. Il modello di Eudosso prevedeva un elevato numero di sfere (27 in totale) ma, con il passare del tempo, si rivelò impreciso: le osservazioni mostravano infatti significative discrepanze tra le posizioni dei pianeti calcolate e quelle effettive. Successivamente, fu Callippo di Cizico (IV secolo a.C.), discepolo della scuola di Aristotele, ad apportare modifiche e perfezionamenti al sistema astronomico di Eudosso, aumentando il numero delle sfere da 27 a 34. I moti apparenti del Sole, dei pianeti e delle stelle risultarono, così, descritti con notevole accuratezza. Callippo, inoltre, indagò scrupolosamente la durata delle lunazioni e dell’anno solare, giungendo alla conclusione che 76 anni solari corrispondono a 940 lunazioni (per altri dettagli sull’applicazione dei calcoli di Callippo al calendario, rimandiamo al percorso Horas doceo. Storia della misurazione del tempo). Il valore da lui ottenuto per una singola lunazione (29 giorni, 12 ore, 44 minuti e 25,5 secondi) si discosta da quello attuale (29 giorni, 12 ore, 44 minuti e 2,9 secondi) di soli 22,7 secondi: un risultato davvero sorprendente. 

La visione astronomica di Eudosso era destinata ad ampia fortuna. In epoca ellenistica, il poeta Arato di Soli (315 a.C. - 240 a.C.) adattò in forma poetica gli scritti originali di Eudosso (purtroppo andati perduti). Nell’opera dal titolo Fenomeni (Φαινόμενα), Arato elenca le costellazioni allora note (con indicazioni circa il loro sorgere e il loro tramontare), descrive il modello delle sfere omocentriche di Eudosso e il percorso del Sole nello Zodiaco ed indica come effettuare le previsioni del tempo meteorologico. Il volume, pur contenendo diverse inesattezze scientifiche, ebbe grande successo: già manuale scolastico di astronomia in età antica, fu l’unica opera di poesia greca a sopravvivere in Occidente durante i secoli medievali. 

Aristotele

Come per Platone, anche nel caso di Aristotele (384-383 a.C. - 322 a.C.) non potremo trattare con esaustività le sue teorie circa la materia astronomica. Accenneremo, quindi, soltanto agli aspetti principali. 

Figura 4. Ritratto di profilo di Aristotele. Libera interpretazione di una statua in marmo conservata presso il Museo Nazionale Romano (a Roma). 

La struttura del cosmo aristotelico è trattata, in particolare, nelle opere Fisica (Φυσικὴ ἀκρόασις) e Sul cielo (Περὶ οὐρανοῦ). Secondo il filosofo, il mondo sublunare (che comprende la Terra, sferica, al suo interno) è composto da quattro elementi (terra, acqua, aria e fuoco) ed è soggetto al divenire e alla corruzione. Ogni elemento tende a rimanere, o a ritornare, nel proprio luogo naturale: la Terra, dunque, essendo composta dagli elementi terra ed acqua, che tendono verso il basso, secondo il filosofo è collocata al centro dell’universo (nella cosiddetta posizione di “basso assoluto”). Aristotele teorizza, quindi, un modello cosmologico geocentrico. 

Figura 5. I quattro elementi del mondo sublunare (fuoco, aria, acqua e terra). Libera interpretazione di un’immagine tratta da un’edizione de De proprietatibus rerum (datata 1491), opera enciclopedica di Bartolomeo Anglico (XIII secolo).

Nell’opera Sul cielo, il filosofo adduce alcune prove della sfericità della Terra, come l’ombra circolare di quest’ultima sulla superficie del nostro satellite durante le eclissi di Luna e l’osservazione di diverse stelle o costellazioni a differenti latitudini.

Figura 6. Una delle prove più utilizzate sin dall’antichità a sostegno della sfericità della Terra: gli alberi e le vele di una nave sono sempre visibili, da lontano, prima dello scafo. Aristotele, tuttavia, non si servì di questa argomentazione. Libera interpretazione di un’immagine tratta da M. Blundeville, His Exercises, containing eight Treatises […] (1613) di Thomas Blundeville (circa 1522 - circa 1606). 

Al contrario del mondo sublunare, le sfere celesti sono composte di una sostanza incorruttibile ed inalterabile (l’etere) e sono regolate da leggi permanenti e immutabili. Aristotele adotta il modello planetario di Eudosso delle sfere omocentriche perfezionato da Callippo, aggiungendo però ulteriori sfere per ciascun pianeta (giungendo ad un totale di 55). Oltre il mondo sublunare si trovano le sfere celesti riferite, rispettivamente, alla Luna, a Mercurio, a Venere, al Sole, a Marte, a Giove, a Saturno e, infine, alle stelle fisse (così denominate in quanto, osservate dalla Terra, appaiono immobili nelle loro posizioni). Quest’ultima sfera è detta “primo mobile” in quanto causa il movimento di tutte le altre sfere concentriche di diametro inferiore. Lo stesso primo mobile è mosso da una causa prima: il primo motore immobile, individuabile in una divinità suprema. Secondo Aristotele, dunque, il movimento dei corpi celesti è descritto dal moto circolare, il più perfetto e regolare; inoltre, secondo il filosofo, l’universo è unico e finito. Com’è noto, il cosmo aristotelico, successivamente perfezionato da Tolomeo (di cui parleremo nella prossima tappa del nostro percorso), fu infine accolto e adattato dalla teologia cristiana.

Eraclide Pontico

Poco più giovane di Aristotele, Eraclide Pontico (385 a.C. - 322 o 310 a.C.) fu filosofo ed astronomo, anch’egli allievo di Platone. Si dedicò a numerose e differenti discipline (etica, fisica, grammatica, retorica, storia, letteratura e musica). Per quanto concerne l’astronomia, fu promotore di idee fortemente innovative. Eraclide pensava, infatti, che i corpi celesti non siano “incastonati” nelle sfere cristalline, bensì che siano liberi di muoversi nell’etere. Inoltre, il moto apparente delle stelle fisse, secondo il filosofo, sarebbe dovuto, in realtà, al moto rotatorio della Terra attorno al proprio asse di rotazione, da occidente verso oriente, nel corso di 24 ore. Infine, nella sua opinione, Mercurio e Venere ruotano attorno al Sole, mentre gli altri pianeti orbitano attorno alla Terra. Come nel caso di Filolao, secondo alcuni studiosi moderni le dottrine di Eraclide potrebbero aver inciso sulla formazione della teoria copernicana. 

Testi e disegni originali di Anna Maragno. Non riprodurre senza autorizzazione.

Note

1. Euripide, Ione, 1145. Con queste parole il drammaturgo descrive il peplo che Ione drappeggia come copertura di una tenda, a simulare la volta celeste. Il tessuto è fitto di immagini che richiamano il cielo, come Urano, Helios, Espero, le Pleiadi, Orione, l’Orsa, le Iadi. Per un’analisi del passo si rimanda a P. Boitani, Il grande racconto delle stelle, Società editrice il Mulino, Bologna, 2012, pp. 39-40.

2. Cicerone (nat. deor. 1,10) attribuisce questa formula alla scuola pitagorica. In età medievale, come è a tutti noto, il detto passò invece a riguardare l’autorità di Aristotele. 

Fonti delle immagini

Figura 1. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.

Figura 2. Fyodor Andreyevich Bronnikov, immagine di pubblico dominio, al link:
https://commons.wikimedia.org/wiki/File:Bronnikov_gimnpifagoreizev.jpg

Figura 3. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.

Figura 4. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.

Figura 5. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.

Figura 6. Disegno originale di Anna Maragno, non riprodurre senza autorizzazione.

Bibliografia e consigli di lettura

Abetti, G., Storia dell’astronomia, Vallecchi, Firenze, 1963

Bersanelli, M., Il grande spettacolo del cielo. Otto visioni dell’universo dall’antichità ai nostri giorni, Sperling & Kupfer, Milano, 2018

Boitani, P., Il grande racconto delle stelle, Società editrice il Mulino, Bologna, 2012

Bowen, A. C., Wildberg, C. (edited by), New Perspectives on Aristotle’s De caelo, Brill, Leiden, Boston, 2009

Brooke-Hitching, E., L’Atlante del Cielo. Le mappe più belle, i miti e le meraviglie dell’universo, tr. it. a cura di V. Gorla, Mondadori, Milano, 2020 

Couprie, D. L., Heaven and Earth in Ancient Greek Cosmology. From Thales to Heraclides Ponticus, Springer, New York, Dordrecht et al., 2011

Graham, D. W., Science Before Socrates. Parmenides, Anaxagoras, and the New Astronomy, Oxford University Press, New York, 2013

Dreyer, J. L. E., A history of astronomy from Thales to Kepler. Revised with a foreword by W. H. Stahl, Second Edition, Dover Publications, New York, 1953

Evans, G., The Astronomy of Heracleides Ponticus, in «The Classical Quarterly» 20, fasc. 1 (1970), pp. 102-111

Gigante, M. (a cura di), Diogene Laerzio. Vite dei filosofi, Laterza, Bari, 1962

Gregory, A., Eudoxus, Callippus and the Astronomy of the “Timaeus”, in «Bulletin of the Institute of Classical Studies», Supplement 78 (2003), pp. 5-28

Hack, M., Ferreri, W., Cossard, G., Il lungo racconto dell’origine. I grandi miti e le teorie con cui l’umanità ha spiegato l’Universo, Sperling & Kupfer, Milano, 2018

Kalachanis, K., Theodosiou, E., Dimitrijević, M. S., Anaxagoras and his contributions to astronomy, in «Astronomical and Astrophysical Transactions» 30, fasc. 4 (2018), pp. 523-530

Kouremenos, T., Plato’s forms, mathematics and astronomy, De Gruyter, Boston, Berlin, 2018

Leopardi, G., Storia dell’astronomia dalla sua origine fino all’anno MDCCCXIII, con uno scritto di A. Massarenti e un’appendice di L. Zampieri, BookTime, Milano, 2008

Maniatis, Y. N., Pythagorean Philolaus’ Pyrocentric Universe: Its Significance and Contribution to Astronomy and Astrophysics, in «ΣΧΟΛΗ. Ancient Philosophy and the Classical Tradition» 3, fasc. 2 (2009), pp. 401-415

Pichot, A., La nascita della scienza. Mesopotamia, Egitto, Grecia antica, tr. it. a cura di M. Bianchi, Edizioni Dedalo, Bari, 1993

Schiaparelli, G. V., Le sfere omocentriche di Eudosso, di Callippo e di Aristotele. Memoria di G. V. Schiaparelli, Letta al Reale Istituto Lombardo di scienze e lettere nell’adunanza del 26 novembre 1874, Hoepli, Milano, Pisa, Napoli, 1875

Timpanaro Cardini, M., Pitagorici antichi. Testimonianze e frammenti, Bompiani, Milano, 2010

Vlastos, G., Plato’s Universe, University of Washington Press, Seattle, 1975