La Relativià Generale è la teoria che forse, più di tutte, ci ha fatto capire come una delle interazioni fondamentali, la gravità, che pensiamo di conoscere meglio perche’ la sperimentiamo quotidianamente, in effetti ha una natura molto peculiare. La connessione con la geometria dello spazio-tempo e l’eleganza della nascita della sua formulazione ad opera di A.Einstein è spiegata in questo percorso che, anche se richiede una maggiore attenzione, ci guidera’ dalla gravitazione newtoniana alle onde gravitazionali.
percorso di Giancarlo Cella
In natura sono note quattro interazioni fondamentali, che spiegano direttamente o indirettamente i fenomeni osservati. Due di esse, dette “interazione forte” e “interazione debole”, sono forse poco note perché legate a fenomeni non associati in modo evidente alla nostra esperienza di tutti i giorni. Nonostante questo sono estremamente importanti: la prima ad esempio è necessaria per la stabilità dei nuclei atomici e quindi per l'esistenza della materia così come la conosciamo. La seconda è indispensabile per permettere alle stelle (e quindi anche al Sole) di produrre energia convertendo idrogeno in elio.
Le altre due interazioni ci sono molto più familiari.
La “interazione elettromagnetica” descrive la forza attrattiva o repulsiva tra cariche, e quindi è responsabile della struttura atomica, dei fenomeni elettrici e magnetici che osserviamo nella vita di tutti i giorni, e anche della radiazione (luce, radio, microonde etc.).
La forza elettrica tra due cariche Q1 e Q2 poste ad una distanza d tra loro è data da
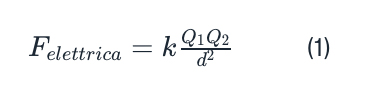
dove k è una costante. La forza è repulsiva se le cariche sono dello stesso segno e attrattiva altrimenti.
La teoria della Relatività Generale ha a che fare con la “interazione gravitazionale”, responsabile della attrazione tra masse. La grande intuizione di Newton, che formulò la legge della Gravitazione Universale, fu che la forza di gravità tra due masse M1 e M2 poteva scriversi come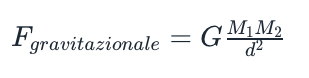
dove G è ancora una costante (la costante di Newton). In questo caso, contrariamente al caso elettromagnetico, la forza è sempre attrattiva. Tra le quattro interazioni, è la più debole. Se paragoniamo la forza elettrica e quella gravitazionale tra due elettroni troviamo
che è un numero enormemente piccolo. Nonostante questo, l'interazione gravitazionale è di gran lunga la più importante quando si considerano fenomeni che avvengono a grande scala (cioè a grandi distanze e che coinvolgono corpi molto grandi), come il moto dei pianeti, delle galassie o dell'Universo nel suo insieme. La ragione di ciò si può capire tenendo conto che cariche uguali si respingono e cariche differenti si attraggono, secondo la legge precedente. Se consideriamo un pianeta avremo una massa molto grande, mentre il numero di cariche positive e negative tenderanno ad equilibrarsi tra di loro: corpi molto grandi hanno grande massa ma tendono a non essere carichi.
La teoria di Newton spiega in modo molto accurato il moto dei pianeti attorno al Sole. Nonostante questo quando Albert Einstein rivoluzionò la nostra comprensione dello spazio e del tempo con la teoria della Relatività Speciale, ci si trovò di fronte ad un problema concettuale.
Consideriamo la forza di attrazione che il Sole esercita sulla Terra: essa è diretta verso il Sole. Supponiamo che per qualche motivo quest'ultimo inizi a spostarsi, a partire da un certo istante. La legge di Newton ci dice che anche la direzione della forza attrattiva sentita dalla Terra inizierà istantaneamente a cambiare, in altre parole abbiamo una azione a distanza.
Ma la Relatività Speciale è incompatibile con una azione a distanza: nessun effetto fisico può propagarsi ad una velocità maggiore di quella della luce, e il tempo necessario a questa per percorrere la distanza Terra–Sole è di circa 8 minuti. Abbiamo dunque una contraddizione, ed è necessario superare la teoria di Newton per ottenere una teoria della gravitazione in accordo con la Relatività Speciale.
La strada da percorrere, in un certo senso, è semplice. Possiamo iniziare ad osservare che anche l'espressione della forza elettrica tra due cariche, espressa dalla Equazione (1) è una azione a distanza. Sappiamo in questo caso che si tratta di una legge valida solo se le cariche sono ferme, o in moto a piccole velocità, un caso particolare di una insieme di equazioni più generali dovute a James Clerk Maxwell.
Non scriveremo le equazioni di Maxwell in dettaglio, ma è importante sottolineare un importante cambio di prospettiva che esse implicano:
• La forza che si esercita su una carica non è dovuta direttamente alle altre cariche presenti, ma all'azione di un campo elettromagnetico. Semplificando un poco, possiamo scrivere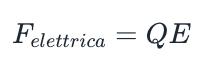 
dove Q è la carica considerata e E il campo elettrico valutato nel punto in cui la carica si trova.
• Il campo elettromagnetico è generato dalle cariche presenti, in un modo descritto dalle equazioni di Maxwell. Ciò che è importante qui è che se una carica si mette improvvisamente in moto, il campo da essa prodotto ad una certa distanza risentirà del cambiamento solo dopo il ritardo necessario a percorrere questa alla velocità della luce. Questo è mostrato dalla animazione in Figura 1, dove il campo elettrico è rappresentato dalle linee tratteggiate (linee di forza).
Figura 1: Il campo elettrico generato da una carica puntiforme (in rosso), rappresentato dalle linee di forza. La carica è messa improvvisamente in moto a velocità costante: il campo della carica in moto sostituisce quello della carica ferma solo dopo un ritardo dovuto al tempo di propagazione dell'effetto alla velocità della luce.
Introducendo il campo elettromagnetico il problema della azione a distanza è superato. Per risolverlo nel caso gravitazionale, potrebbe quindi essere sufficiente introdurre un opportuno “campo gravitazionale” e determinare le equazioni necessarie a descriverlo. Questo compito porterà Albert Einstein alla formulazione della teoria della Relatività Generale, che offrirà una descrizione dello spazio e del tempo strettamente connessa a quella della Relatività Speciale, ma ancora più rivoluzionaria.