4. Relatività generale

percorso di Giancarlo Cella

Per comprendere intuitivamente alcuni aspetti della Relatività Generale è utile considerare una particolare rappresentazione grafica, detta diagramma spazio–temporale. Un esempio è riportato in Figura 4.
Abbiamo due assi: quello orizzontale corrisponde ad una coordinata spaziale, quello verticale ad una coordinata temporale.
Ogni punto nel diagramma corrisponde ad un evento, ossia a qualcosa che accade in una posizione e ad un istante ben determinati. Ad esempio l'evento P avviene al tempo t=2 (misurato in secondi) nella posizione r=1 (misurata in secondi–luce).

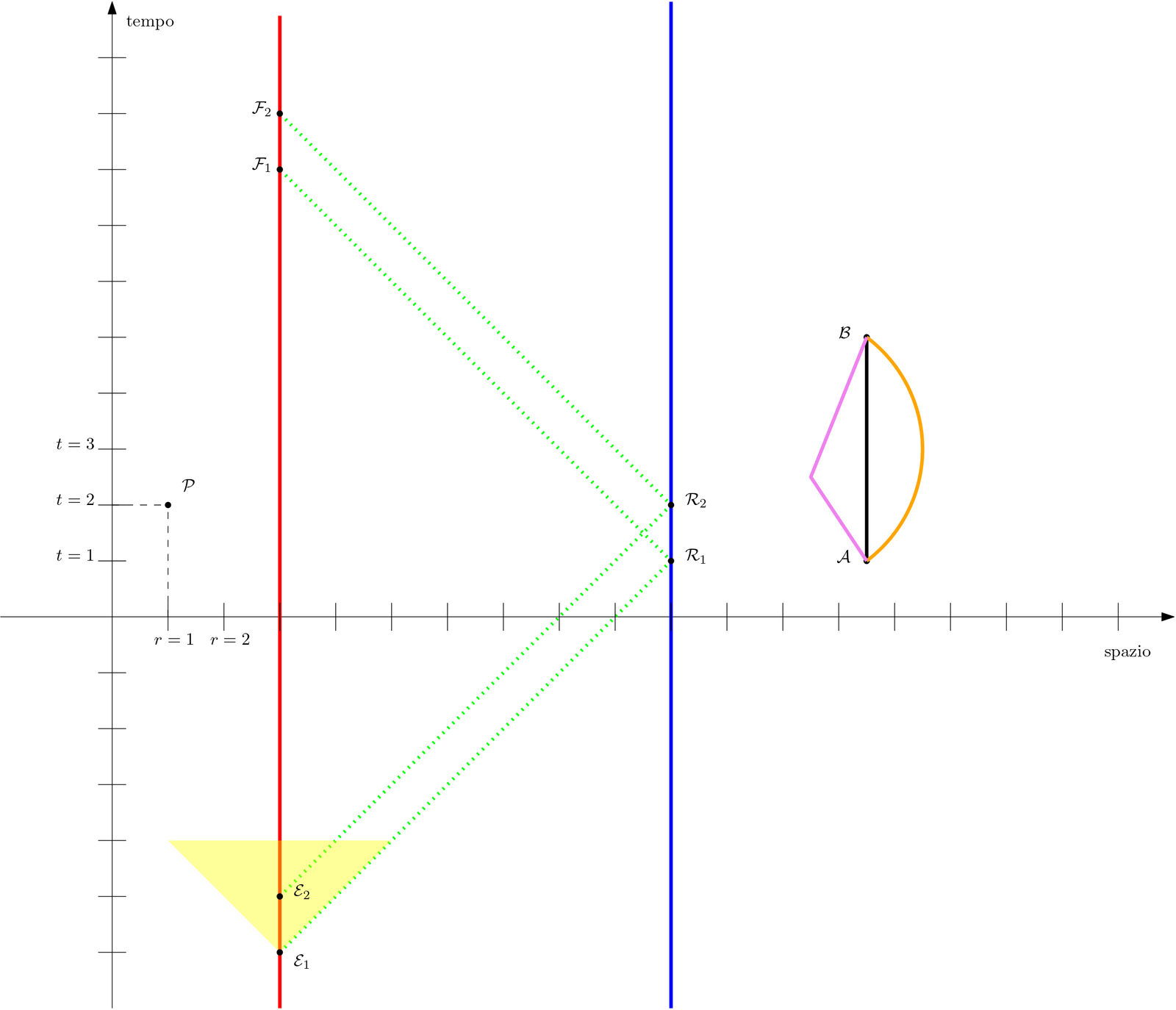Figura 4: Il diagramma spazio–temporale delle linee di universo di due particelle (rossa e blu) che rimangono alla stessa coordinata spaziale al passare del tempo. Le linee tratteggiate corrispondono alle linee di universo di due lampi luminosi che partono dalla particella rossa (eventi E₁ e E₂ ), sono riflessi dalla particella blu (eventi R₁ e R₂ e tornano a quella rossa (eventi F₁ e F₂). Dato che misuriamo lo spazio in secondi–luce, e che i lampi luminosi si muovono alla velocità della luce, le relative linee di universo sono inclinate di 45° rispetto all'orizzontale: lo spazio percorso è numericamente uguale al tempo trascorso. In giallo è rappresentato il cono luce dell'evento E₁ : dato che niente può muoversi ad una velocità maggiore di quella della luce qualsiasi particella o segnale emesso in E₁ avrà una linea di universo contenuta nel cono luce. Sono inoltre rappresentate alcune possibili linee di universo di una particella che si propaga dall'evento A all'evento B.

La linea rossa in Figura 4 rappresenta una particella che, al passare del tempo, rimane alla stessa coordinata r=3 . Possiamo chiamarla linea di universo della particella rossa.
Lo stesso vale per la linea blu, che rimane alla coordinata r=10.
Le linee tratteggiate corrispondono invece a segnali luminosi inviati dalla particella rossa. Più esattamente, gli eventi E₁ e E₂ rappresentano l'emissione di due lampi luminosi, al tempo t=-6 e t=-5 rispettivamente, da parte della particella rossa.
Con le unità di misura scelte, un segnale che si muove alla velocità della luce si propagherà su una linea di universo inclinata di 45° rispetto all'orizzontale. Il diagramma si riferisce ad una situazione nella quale la gravitazione è assente.
Qual'è il significato delle coordinate scelte? Per capirlo, immaginiamo di avere scelto per t il tempo segnato da un orologio che si muove insieme alla particella rossa, e decidiamo arbitrariamente che questa è fissa a r=3 . Occorre trovare un modo ragionevole per determinare le coordinate di un qualsiasi altro evento, ad esempio delle riflessioni R₁ e R₂.
Possiamo ragionare in questo modo: siamo in grado di misurare le coordinate delle emissioni E₁ e E₂, e anche degli eventi che corrispondono alla ricezione dei lampi riflessi F₁ e F₂. La distanza di R₁ ad esempio sarà la metà del tempo trascorso tra emissione e ricezione diviso per la velocità della luce, che nelle nostre unità è c=1 . Quindi

Invece il tempo a cui avviene la riflessione sarà a metà strada tra l'emissione e la ricezione, ossia

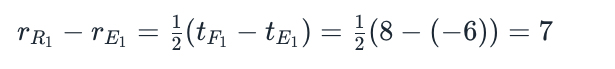
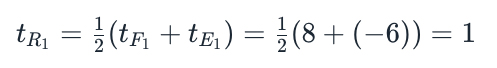
Similmente per R₂, come si può facilmente verificare. Come si vede le coordinate degli assi corrispondono alla definizione data.
Diamo adesso una definizione un poco particolare delle linee di universo seguite da particelle libere. Consideriamo due eventi A e B: tra tutte le linee di universo che iniziano in A e finiscono in B, quella seguita da una particella libera è di durata massima, se la misuriamo con un orologio che si muove con essa. Facendo riferimento alla Figura 4, vediamo tre possibili linee di universo che uniscono i due eventi. Chiaramente l'orologio trasportato lungo la linea nera (sempre in quiete in questo caso) misurerà un tempo maggiore di quelli trasportati lungo le altre due, dato che questi sono in moto e secondo la relatività speciale un orologio in moto rallenta rispetto a uno in quiete. La “strana” definizione data ha un grande vantaggio: è indipendente dalle coordinate scelte per la rappresentazione. È cioè di carattere puramente geometrico.
Possiamo utilizzarla per ottenere la generalizzazione che cerchiamo: anche in presenza di gravitazione le linee di universo di particelle in caduta libera godranno della stessa proprietà.
Vediamo se tutto ciò ha senso.
Immaginiamo di porre in r=0 una massa (ad esempio una stella). Abbiamo visto che il tempo “rallenta” in prossimità delle masse: intuitivamente per rendere massimo il tempo trascorso non converrà più muoversi da A a B lungo la linea di universo nera, ma piuttosto lungo quella arancio: si perderà qualcosa a causa della velocità non nulla, che farà rallentare l'orologio, ma si potrà compensare e alla fine guadagnarci muovendosi in regioni più lontane dalla massa centrale.
La linea di universo seguita corrisponderà al miglior compromesso, ed è detta geodetica. Corrisponde all'idea intuitiva che per far passare da B la particella è necessario lanciarla un poco verso l'esterno, in modo da compensare l'effetto gravitazionale della massa.
L'aspetto estremamente importante del punto di vista scelto è che non abbiamo più bisogno di parlare di forza di gravità: la linea di universo seguita è determinata esclusivamente da una proprietà geometrica dello spaziotempo.