percorso di Giancarlo Cella
Una importante applicazione della Relatività Generale è la descrizione dell'Universo nella sua interezza.
A prima vista potrebbe sembrare un programma senza speranza, data la complessità e la varietà delle strutture presenti. Possiamo però supporre che, ignorando il dettaglio, sia possibile considerare l'Universo, almeno in prima approssimazione, omogeneo ed isotropo.
Occorre chiarire che ci stiamo riferendo a isotropia e omogeneità spaziale: si presume che ad una certa epoca l'Universo appaia lo stesso in qualsiasi direzione si guardi (isotropia) e qualunque sia il punto di osservazione (omogeneità), per lo meno se consideriamo le proprietà medie su regioni abbastanza grandi.
Invece l'Universo non deve essere necessariamente lo stesso in epoche differenti.
Per descrivere una soluzione di questo tipo dobbiamo cercare soluzioni delle equazioni di Einstein con questa proprietà.
Se in una data epoca le proprietà geometriche (descritte da Gμν) dello spazio dovranno essere le stesse ovunque e in ogni direzione, anche la distribuzione di materia ed energia (descritta da Tμν) dovrà: essere considerata omogenea ed isotropa. In sostanza stiamo trattando il contenuto dell'Universo come un fluido omogeneo e uniforme, costituito da diverse componenti.
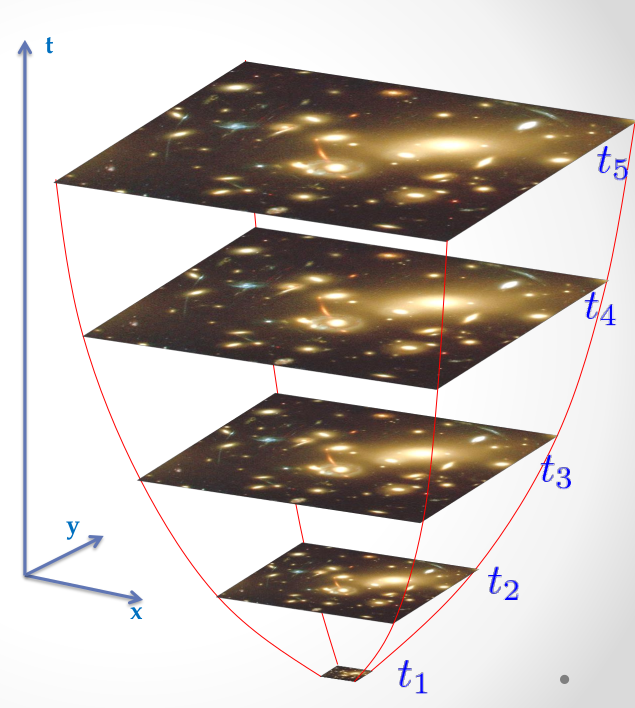
Figura 9: Rappresentazione dello spaziotempo di un Universo in espansione. Ad ogni istante l'Universo è approssimativamente omogeneo ed isotropo. La geometria deve quindi essere la stessa, a meno di un fattore di scala: nel caso considerato le “sezioni” spaziali non sono curve, ma l'intero spaziotempo lo è.
La distorsione della geometria indotta dalla materia dovrà
- dipendere solo dal tempo, dato che abbiamo distribuito uniformemente la massa. In altre parole tutti i coni luce corrispondenti ad eventi simultanei avranno la stessa forma;
- essere tanto maggiore quanto più alta la densità di massa e energia.
Segue che, ad un istante dato, la curvatura dello spazio dovrà essere la stessa in ogni punto. Possiamo aiutare l'intuizione immaginando che lo spazio abbia solo due dimensioni, e quindi sia rappresentabile come una superficie. Abbiamo solo tre possibilità:
1. La curvatura spaziale è nulla. In questo caso lo spaziotempo può essere rappresentato come in Figura 9.
2. La curvatura spaziale è positiva. In questo caso vale la rappresentazione in Figura 10. Notare che l'Universo è spazialmente limitato: se iniziamo a muoverci in una direzione, dopo un poco torniamo al punto di partenza.
3. La curvatura spaziale è negativa. In questo caso non è possibile rappresentare la superficie spaziale in una figura.
In ciascun caso, se l'Universo deve mantenersi isotropo e omogeneo potrà cambiare la propria geometria solo per un fattore di scala: le equazioni di Einstein si semplificano, e permettono di determinare l'evoluzione di questo fattore di scala. Sappiamo che l'Universo si stia espandendo: questo implica che la densità di massa e energia varierà nel tempo secondo una legge che dipenderà dalle caratteristiche del fluido contenuto. La Relatività Generale ci permette, in linea di principio, di determinare quale sarà il destino dell'Universo. Esiste in particolare una interessante relazione tra la curvatura spaziale dell'Universo e la sua evoluzione futura:
- Se la curvatura spaziale è negativa o nulla, l'Universo continuerà a espandersi.
- Se la curvatura spaziale è positiva, ad un certo momento l'Universo smetterà di espandersi e inizierà a contrarsi.
A quanto sembra la curvatura spaziale del nostro Universo è nulla.
Viceversa, andando indietro nel tempo, la densità di energia aumenterà, e l'Universo si contrarrà sempre più rapidamente. Si può mostrare che secondo la Relatività Generale questo processo conduce necessariamente ad una singolarità: muovendosi indietro nel tempo si arriva dopo un tempo finito ad un momento nel quale l'Universo collassa, e la densità di materia diviene infinita. Questo momento viene indicato convenzionalmente come “Big Bang”. Occorre osservare però che prima di raggiungere questa singolarità, l'Universo avrà una energia e una temperatura tali da non permettere più di applicare la Relatività Generale: in verità non abbiamo ancora una teoria valida in questo regime.
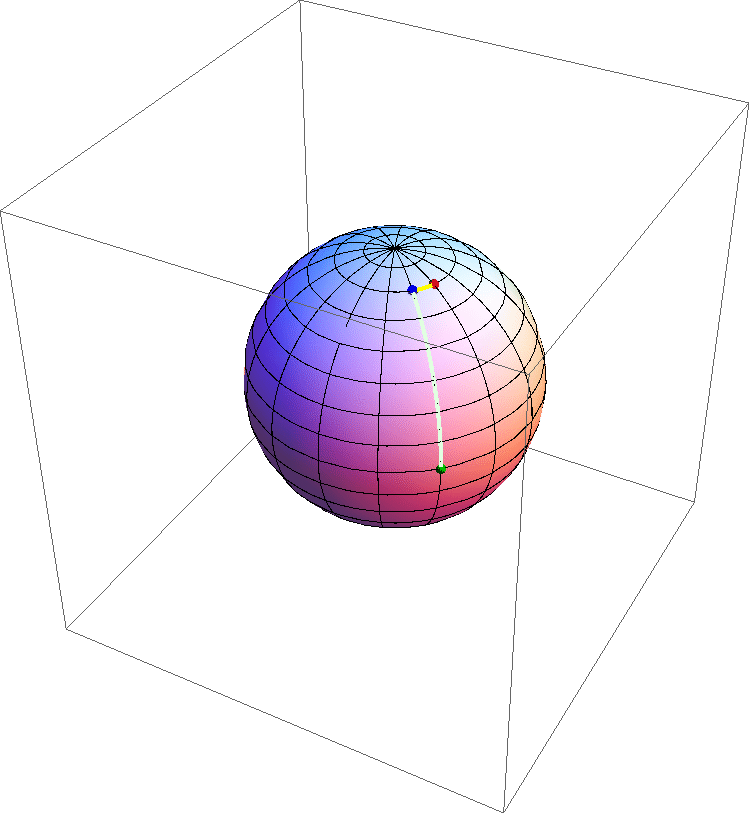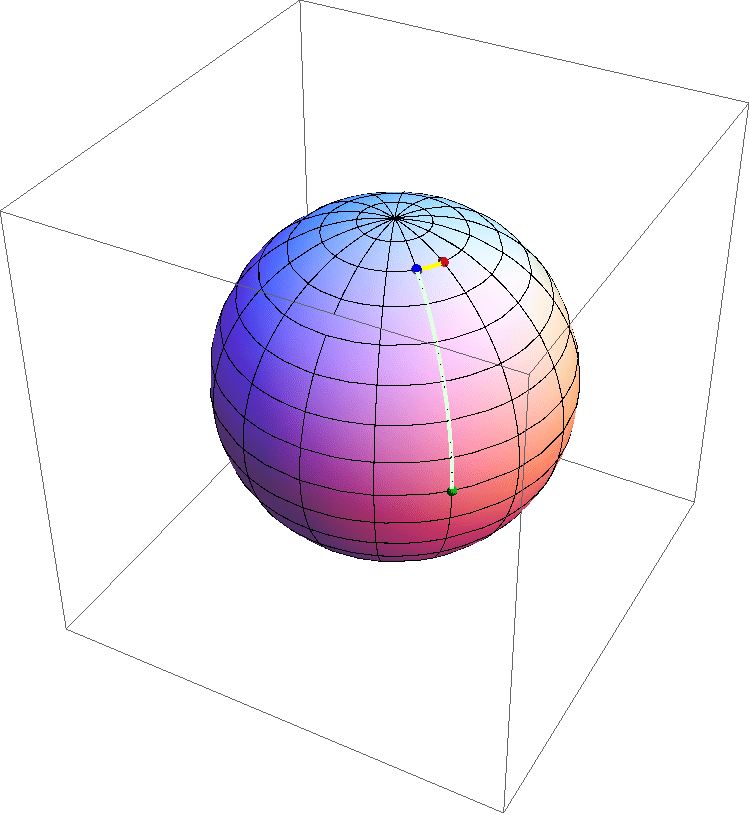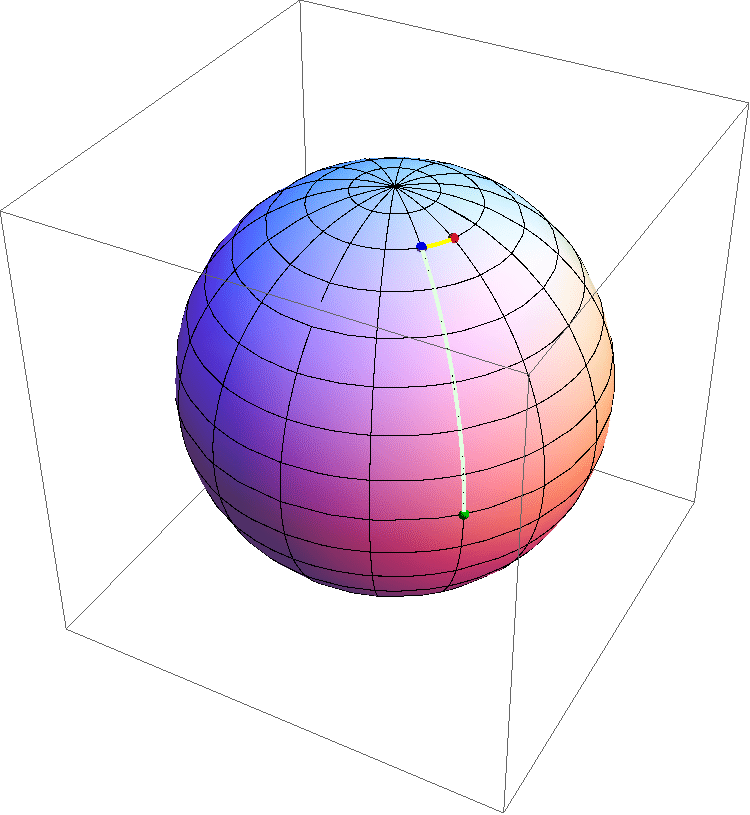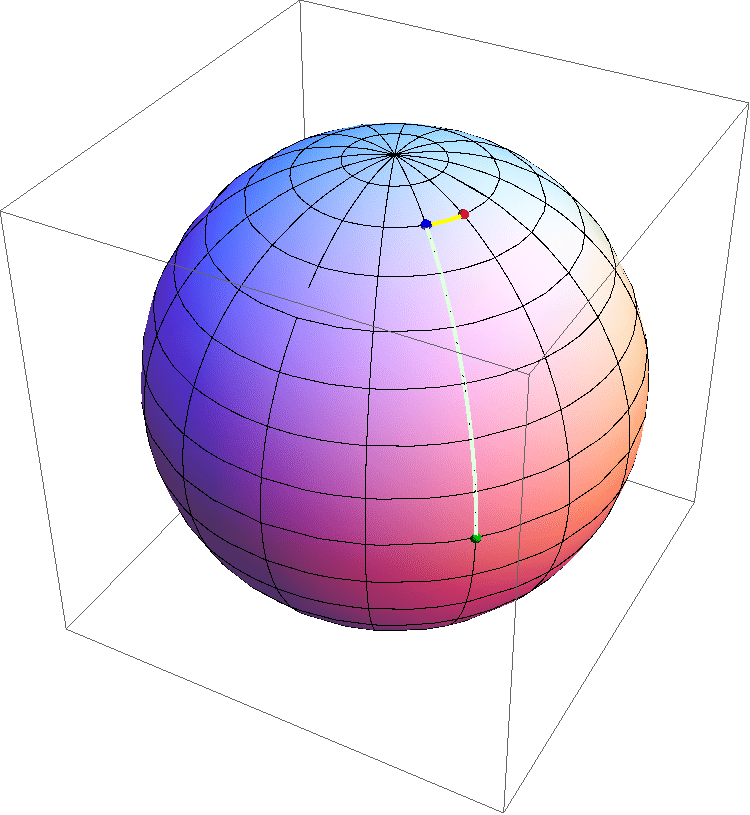Figura 10: un'animazione schematica che mostra l'espansione di una sezione spaziale di un Universo con curvatura positiva al variare del tempo. A causa dell'omogeneità e isotropia la sezione può essere rappresentata da una superficie sferica. Notare che durante l'espansione la curvatura diminuisce, e che ogni punto si allontana da ogni altro nello stesso modo, ad una velocità proporzionale alla distanza.