percorso di Giancarlo Cella
La Relatività Generale si può riassumere nell'equazione di Einstein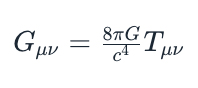 
Senza entrare nei dettagli matematici, possiamo riassumere brevemente alcuni aspetti qualitativi contenuti in questa espressione:
- Gμν è un oggetto matematico, il tensore di Einstein, che descrive la geometria dello spaziotempo.
- Tμν descrive invece la distribuzione della massa (e dell'energia, dato che la relatività speciale ci dice che c'è equivalenza tra l'una e l'altra).
L'equazione ci dice sostanzialmente, ed in modo matematicamente preciso, che la curvatura dello spaziotempo è generata dalla massa e dall'energia in esso presente. Al tempo stesso, prescrive anche come la materia e l'energia si deve muovere in uno spaziotempo di geometria data.
Citiamo liberamente una frase del fisico John Wheeler: La materia dice allo spaziotempo come si deve curvare, e lo spaziotempo dice alla materia come si deve muovere (cioè lungo geodetiche).
L'apparente semplicità della relazione non deve trarre in inganno: si tratta in realtà di un modo compatto di scrivere una serie di equazioni che risultano molto difficili da risolvere. Parte della difficoltà è dovuta alla loro natura non lineare. Se consideriamo le equazioni analoghe per l'elettricità e il magnetismo, le equazioni di Maxwell, vediamo che queste sono invece lineari. Questo significa che, trovate due soluzioni, possiamo combinarle insieme e ottenerne una terza. Ad esempio, due soluzioni potrebbero rappresentare due fasci luminosi che si muovono in certe direzioni: combinandole assieme otteniamo una nuova soluzione che rappresenta i due fasci presenti allo stesso tempo, che magari si intersecano, ma senza disturbarsi. Sfruttando questa proprietà diviene molto più semplice costruire soluzioni con le caratteristiche volute.
Questa proprietà non vale per l'equazione di Einstein: se troviamo due soluzioni e le combiniamo, ciò che otteniamo non è più necessariamente una buona soluzione.
Si conoscono alcune soluzioni particolari di grande importanza, che discuteremo più avanti, valide in situazioni significative che ci si aspettano vicine a casi reali.
Per studiare fenomeni più complessi si possono risolvere le equazioni numericamente, utilizzando calcolatori molto potenti. Per questa via si ottengono risultati ormai piuttosto accurati che possono essere confrontati con risultati sperimentali, come vedremo quando accenneremo alle onde gravitazionali.