percorso di Giancarlo Cella
Quali sono le caratteristiche geometriche dello spaziotempo in presenza di gravitazione?
Per rispondere a questa domanda prendiamo ancor più sul serio le linee geodetiche, affermando che esse sono le “linee rette” dello spaziotempo. Una obiezione naturale è che non sembrano affatto linee rette, ma potremmo rispondere dicendo che non sembrano tali a causa di una scelta sbagliata delle coordinate del diagramma.
Affinché questa risposta sia sensata, è necessario capire se è possibile scegliere nuove coordinate tali da trasformare tutte le linee geodetiche in evidenti linee rette. Ripensando alla discussione delle particelle all'interno della cabina in caduta libera dovrebbe essere chiaro che questo in generale non accade. Possiamo confrontare due casi per capire meglio:
1. Due particelle partono da ferme a quote diverse, in un campo gravitazionale costante. Il campo gravitazionale non dipende dal tempo, quindi data una linea geodetica ne possiamo ottenere un'altra con una traslazione lungo l'asse dei tempi. E dato che il campo è costante, da una geodetica ne possiamo ottenere un'altra anche con una traslazione lungo l'asse spaziale (Figura 5-a). Segue che due geodetiche inizialmente parallele lo rimangono sempre.
2. Due particelle partono da ferme a quote diverse, nel campo gravitazionale di un pianeta. In questo caso il campo gravitazionale diminuisce allontanandosi dal pianeta. Segue che traslando una geodetica lungo l'asse temporale se ne ottiene un'altra, ma non traslandola lungo l'asse spaziale (Figura 5-b). Questo significa che le geodetiche, inizialmente parallele, non lo saranno successivamente: le particelle si allontanano, e questo è un effetto fisico che non è possibile eliminare con una diversa scelta di coordinate.
Il secondo esempio ci fa capire che nello spaziotempo, in presenza di un campo di gravità non costante, la geometria non può essere piatta: abbiamo a che fare con uno spaziotempo curvo. Possiamo pensare per analogia alla superficie di una sfera.
In questo caso le geodetiche sono cerchi massimi (ad esempio i meridiani) che pur essendo paralleli all'equatore, in seguito convergono.
Un osservatore che vede una piccola parte della sfera da vicino ha difficoltà a riconoscere che si tratta di una superficie curva: in altre parole gli effetti della curvatura si annullano localmente, come accade per quelli gravitazionali.
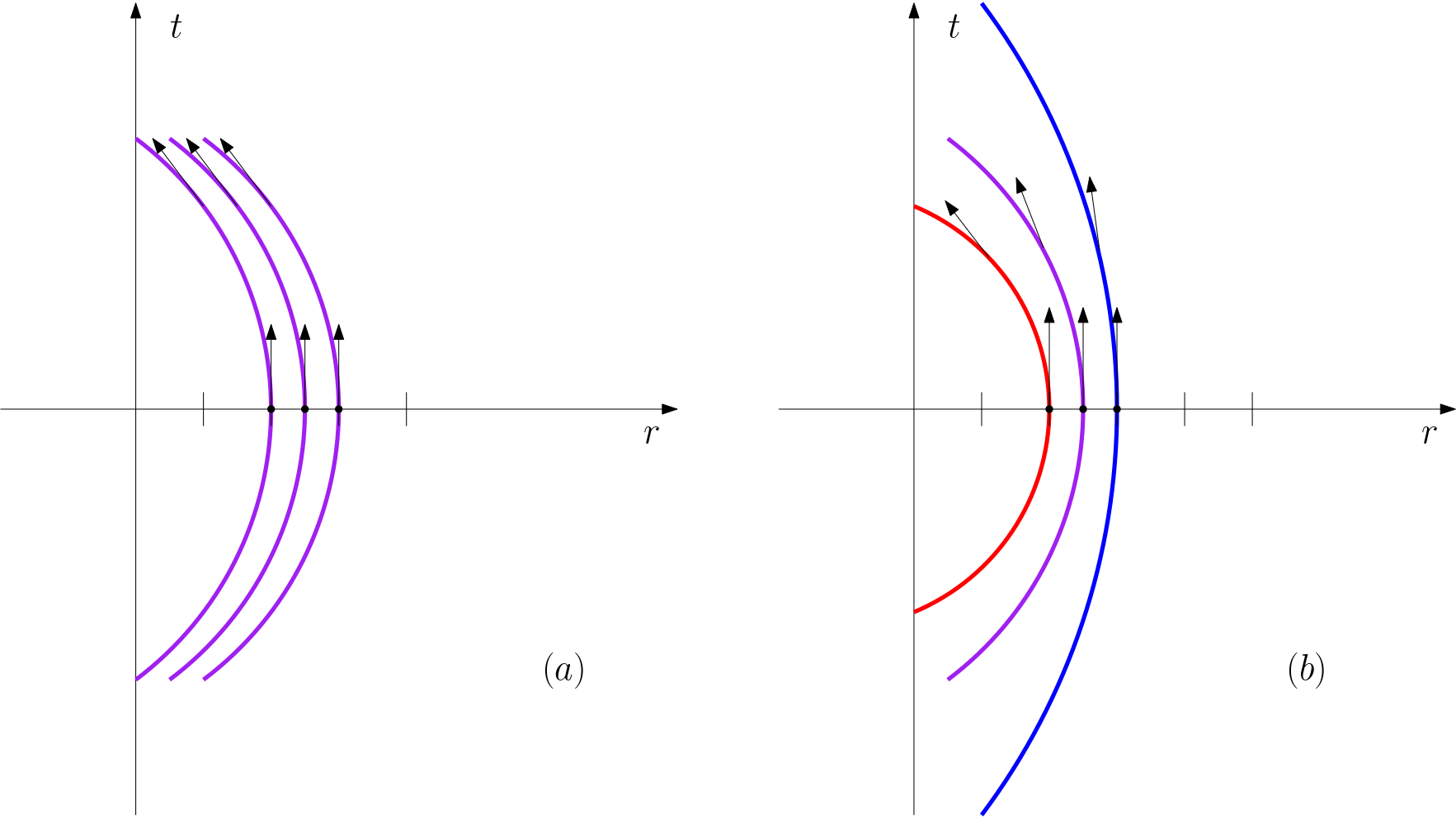
Figura 5: Linee di universo geodetiche di tre particelle lanciate da altezze diverse ( r ) in un campo gravitazionale costante (a sinistra) e in un campo che si indebolisce all'aumentare della distanza r . Nel primo caso tutte le geodetiche si possono sovrapporre con una traslazione lungo l'asse spaziale, e quindi le particelle rimangono a distanza costante. Nel secondo questo non è possibile, e la distanza tra le particelle cambia nel tempo.
Come ulteriore esempio, consideriamo il diagramma spaziotempo di alcuni pianeti in orbita attorno al Sole. Questo è rappresentato in Figura 6.
In questo caso abbiamo due coordinate spaziali e una temporale (l'asse temporale è verticale).
La linea di universo del Sole, in quiete, è quella verticale. Attorno si sviluppano le linee di universo dei pianeti: si tratta in tutti i casi di geodetiche, cioè di “linee rette” in uno spaziotempo curvato dalla presenza della massa del Sole. Come ci si può aspettare intuitivamente, allontanandosi dal Sole gli effetti gravitazionali sono meno importanti, e quindi la curvatura dello spaziotempo diminuisce. Di conseguenza le linee di universo appaiono sempre più rettilinee.
Newton avrebbe interpretato questo diagramma dicendo che le linee di universo dei pianeti sono curvate dalla forza attrattiva del Sole. Dal punto di vista di Einstein, tutte le linee di universo sono “rettilinee” (cioè, geodetiche), ma in uno spaziotempo curvato dalla massa del Sole.
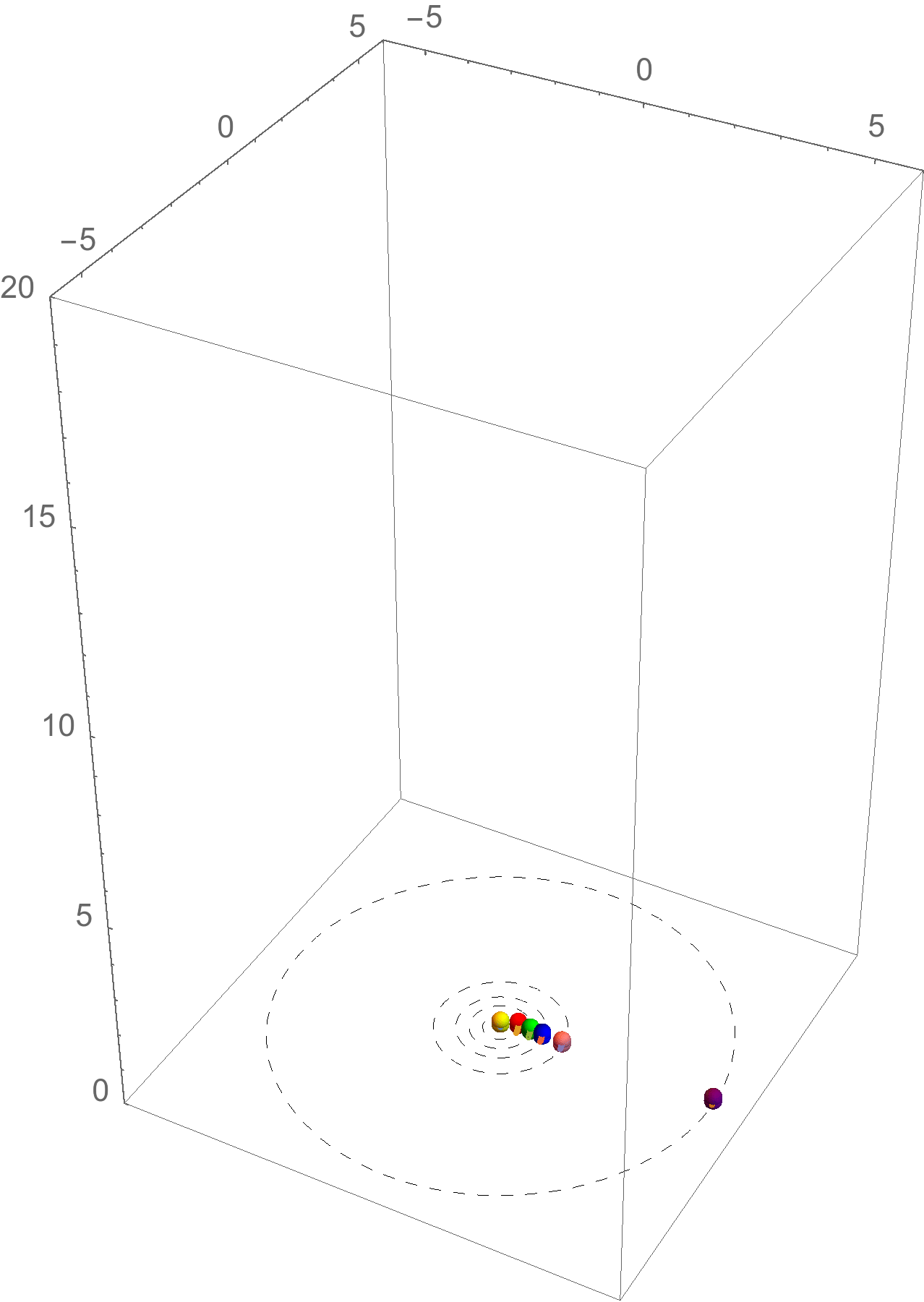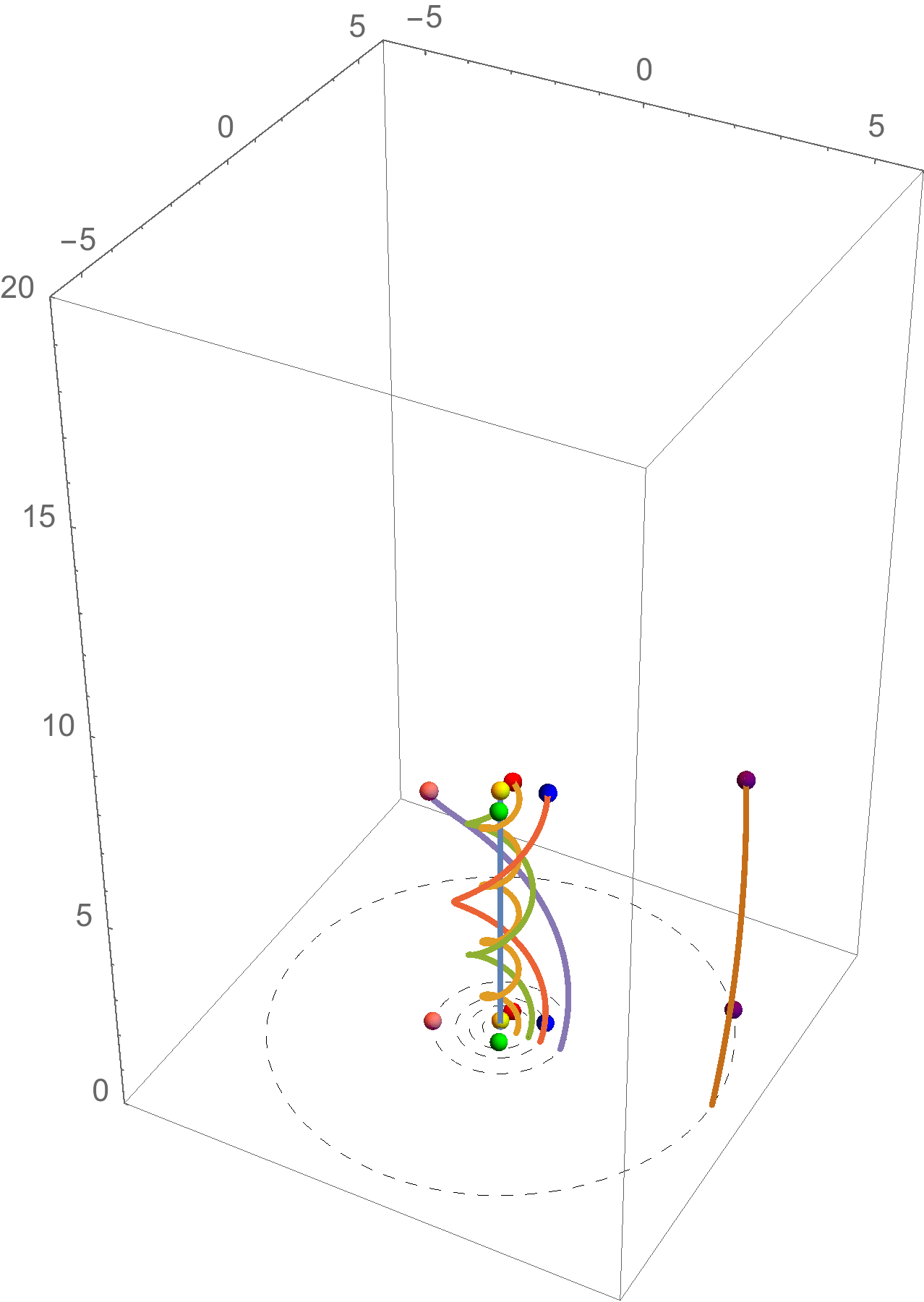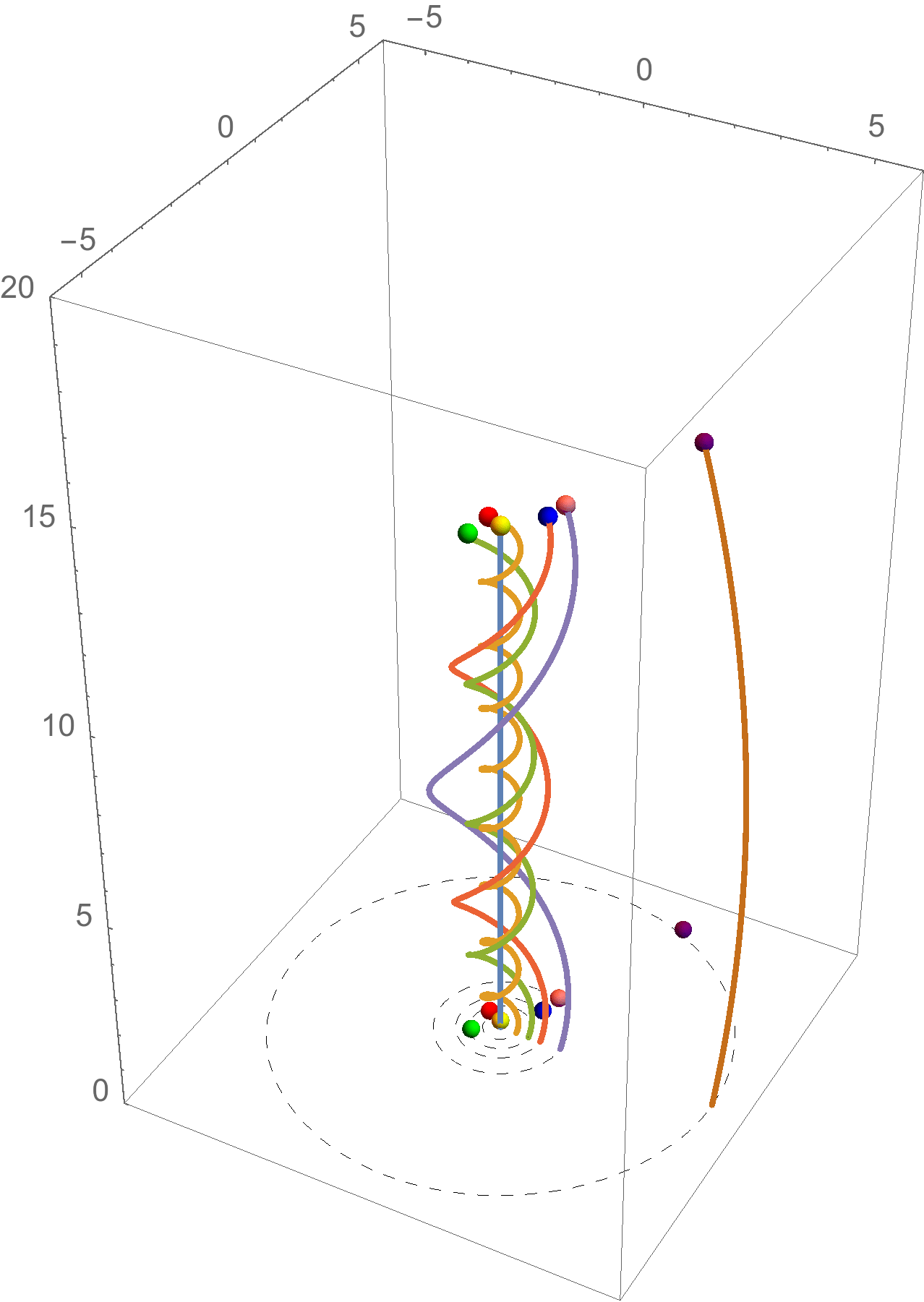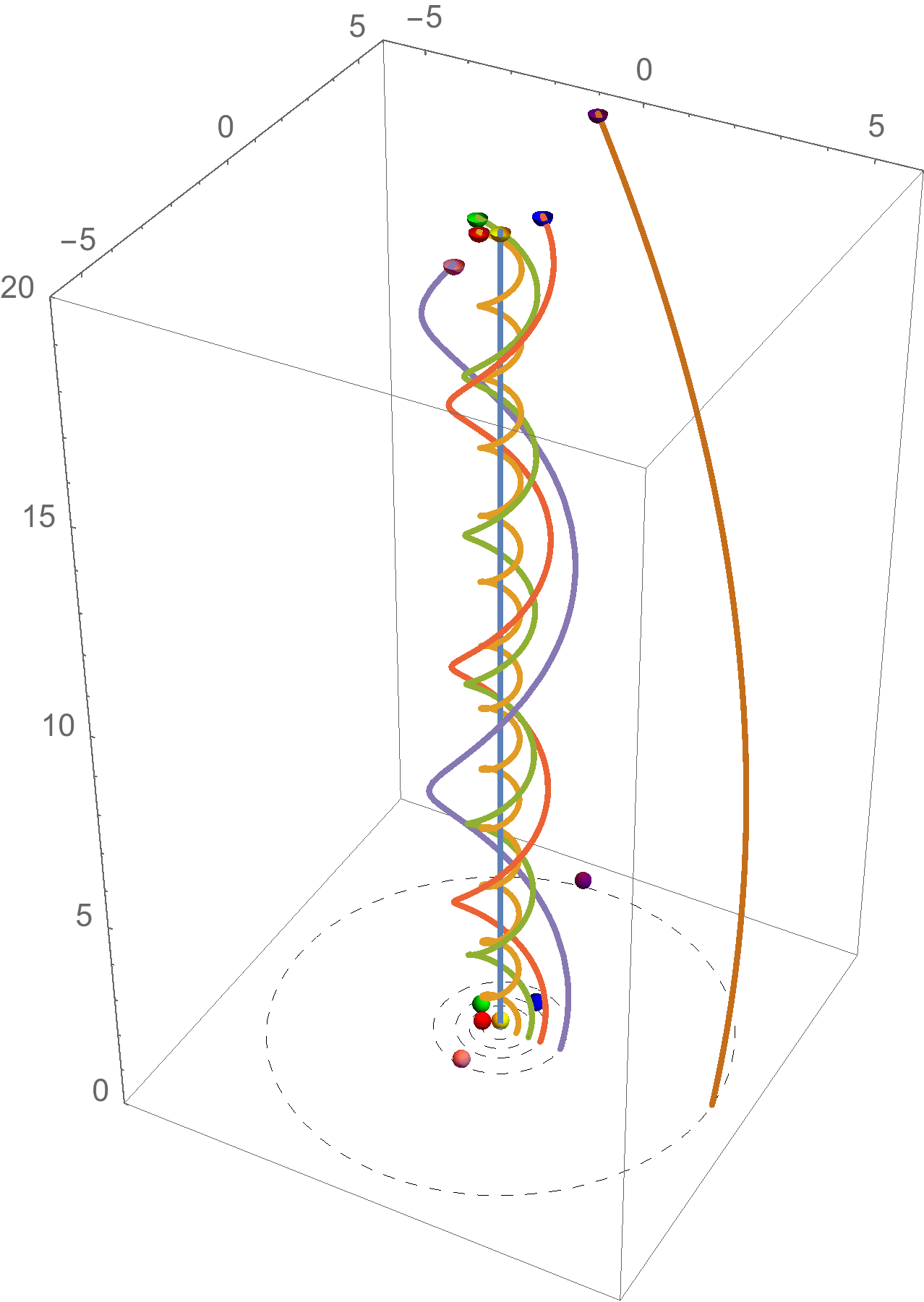
Figura 6: Le linee di universo del Sole (verticale e azzurra) e dei pianeti più vicini. Le scale dei tempi e delle distanze sono scelta in modo da rendere evidente l'effetto: se i tempi fossero misurati in secondi e le distanze in secondi luce tutte le linee di universo sarebbero indistinguibili da linee rette.

