di G. Bormetti, C.M. Carloni Calame, G. Montagna, N. Moreni, O. Nicrosini, M. Treccani
La legge empirica di Zipf che si incontra nello studio delle proprietà statistiche del linguaggio umano e del DNA è un esempio di cosiddetta legge di potenza. Una legge di questo tipo è caratteristica di quelle distribuzioni di probabilità studiate per primo dal matematico francese Paul Lévy 
intorno agli anni ’30 del secolo scorso e per questo note come distribuzioni di Lévy.
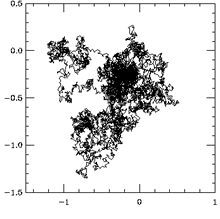
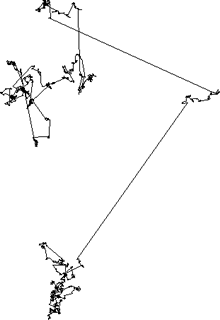
Le variabili stocastiche descritte da queste distribuzioni di probabilità percorrono dei cammini irregolari e caotici (detti voli di Lévy) simili a prima vista - ma in realtà diversi se esaminati in maggiore dettaglio - a quelli della particella browniana che abbiamo già incontarto. Queste differenze si possono osservare chiaramente confrontando le due figure qui sotto, ottenute mediante simulazioni al computer: la figura a sinistra rappresenta il moto di una particella browniana in due dimensioni, mentre la figura a destra è la rappresentazione di un volo di Lévy.
|
|
|
| Moto browniano | Volo di Lévy |
Dal confronto fra queste due figure è possibile notare la diversa struttura spaziale dei due moti fortemente irregolari e, in particolare, come i voli di Lévy possono dare origine a dei “salti” di ampiezza più elevata rispetto a quelli più brevi del moto browniano ordinario. Per questo motivo, il moto browniano è un processo di diffusione normale, mentre i voli di Lévy sono un esempio di processo di super-diffusione. La cosa interessante è che molti fenomeni complessi che avvengono in natura presentano caratteristiche molto simili ai voli di Lévy e danno perciò origine a leggi di potenza.