di G. Bormetti, C.M. Carloni Calame, G. Montagna, N. Moreni, O. Nicrosini, M. Treccani
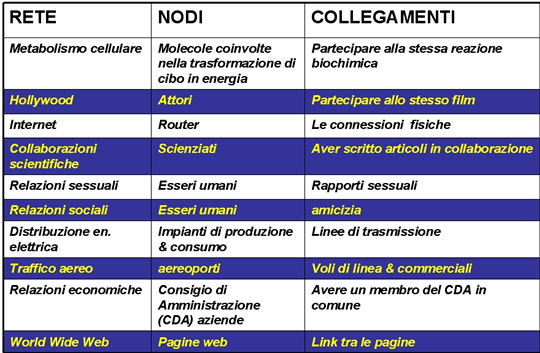
In alcuni sistemi complessi le caratteristiche fondamentali sono descritte non dai punti ma dalle relazioni tra essi. Prendiamo per esempio internet. In questo caso i nodi sono le pagine WEB ed i collegamenti sono i link ad altre pagine. Per comprendere quali sono i siti più importanti è necessario dunque cercare i siti che hanno più collegamenti.
Per trovare un modello che descriva la struttura di queste reti sarebbe necessario tenere conto delle motivazioni che spingono un sito a collegarsi ad un altro (un modello “microscopico”). Tuttavia risulta al momento proibitivo sviluppare un modello in grado di descrivere tale situazione. Allora ciò che si cerca è un modello semplificato della struttura delle reti (un modello “macroscopico”) che, partendo da semplici assunti, sia in grado di descrivere questo fenomeno così complesso.
La teoria delle reti ha una tradizione che risale al 1700 con i primi studi di Eulero
, il quale pone i fondamenti della descrizione matematica delle reti: la teoria dei grafi. Uno dei primi modelli di reti proposto risale agli anni ’60 ed è la rete aleatoria o “democratica” descritta da Erdös 
Rényi . Questo tipo di rete descrive una sistema costituito da un numero fissato di nodi che hanno un valore medio di collegamenti, o grado, ben preciso. In questi tipi di reti i vari nodi sono indistinguibili gli uni dagli altri, in quanto hanno praticamente tutti lo stesso grado, da qui il termine reti “democratiche”.Le reti democratiche hanno il pregio di essere semplici nella costruzione, ma non sono adatte a descrivere le reti reali.
Verso la fine degli anni ’90 è stato proposto un modello estremamente semplice ma efficace che permette di descrivere alcune delle caratteristiche principali delle reti che ritroviamo in natura, nelle scienze sociali e in biologia. Questo modello si basa su due assunti principali: la rete è in continua crescita ed inoltre chi apre un nuovo sito preferisce collegarlo a siti che hanno già un alto numero di connessioni. Quest’ultimo assunto è noto anche come effetto Matteo, riferendosi al passo nel vangelo (Matteo, 25:29) nel quale si afferma “così a chi ha sarà dato e sarà nell’abbondanza”.
Grazie a questi semplici assunti è possibile costruire una rete dove esistono, al contrario dei primi modelli di reti democratiche, pochi nodi che hanno un numero altissimo di connessioni, diventando così il cuore della rete.
Reti con questa struttura si dicono scale-free.
Leggi di potenza e piccoli mondi
Contando il numero di nodi che nella rete hanno lo stesso numero di connessioni si ottiene una legge di potenza: infatti esistono molti nodi che hanno poche connessioni, e pochi nodi che hanno molte connessioni. Questa particolare legge rimane inalterata aumentando il numero di nodi della rete, cioè risulta indipendente dalla grandezza o scala della rete; da qui il nome scale-free.
n° di nodi con K connessioni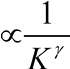 
Il coefficiente ? che compare nella formula è diverso in tipi di reti differenti, ma risulta quasi sempre compreso tra 1 e 3.
Accanto al grado di connettività delle reti un’altra caratteristica fondamentale è il diametro della rete che misura il numero di collegamenti necessario per connettere due nodi qualsiasi. I primi studi quantitativi sulle reti sociali che misurano questa proprietà risalgono agli anni ’60. In questo contesto, i nodi rappresentano le persone ed il collegamento la conoscenza dei due individui. Negli USA, il sociologo Stanley Milgram escogitò un esperimento che permettesse di rivelare la rete di conoscenze “navigando” tra i vari nodi: inviò ad un certo numero di persone che vivevano sulla costa orientale delle lettere chiedendo di spedirle a loro volta a dei conoscenti in modo che queste lettere arrivassero a Chicago attraverso una catena di amici di amici.
Il risultato fu sorprendente, in quanto notò che la maggior parte delle lettere passava attraverso sei persone prima di arrivare a dei conoscenti a Chicago.
È quello che si chiama effetto small world.
Pur essendo costituita da milioni di nodi, la distanza tra due nodi qualsiasi è molto piccola e praticamente indipendente dalla grandezza della rete! Volendo fare un esempio la “distanza” tra un cittadino italiano qualsiasi e il presidente degli USA è mediamente di sei strette di mano. Sembra strano ma è vero!
Universalità delle reti
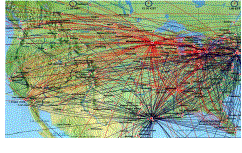
La rete dei collegamenti degli aeroporti USA
I modelli che abbiamo descritto, oltre a riprodurre gli effetti di scale-free e small world hanno permesso di evidenziare una proprietà che non era stata precedentemente osservata, ovvero la solidità delle reti. In una rete di tipo scale-free possono avvenire dei guasti che disattivano un nodo e di conseguenza i suoi collegamenti. Scegliendo in modo casuale il nodo da disattivare, vi è una buona probabilità che tale nodo non sia rilevante, poiché sono pochissimi i nodi con un grado di connettività talmente alto da “garantire” la solidità della rete.
Viceversa, ad un “attacco” mirato, la rete porge il suo tallone d’Achille: conoscendo i suoi nodi più importanti, un pirata informatico riesce ad oscurare l’intera rete attaccando pochi punti ma ben collegati. L’effetto small world è stato studiato per la prima volta nelle reti sociali mentre lo studio della rete WorldWideWeb ha evidenziato la natura scale-free.
Queste due caratteristiche si ritrovano con sorprendente regolarità in reti nate in contesti differenti che spaziano dalle scienze sociali al metabolismo cellulare, toccando anche il mondo del cinema e delle collaborazioni scientifiche. Utilizzando così un modello estremamente semplice, è possibile descrivere e classificare i vari tipi di reti, non in funzione del loro particolare campo di applicazione ma grazie a concetti “universali” - come ad esempio il coefficiente γ della legge di potenza o la distanza media tra due nodi qualsiasi.