di G. Bormetti, C.M. Carloni Calame, G. Montagna, N. Moreni, O. Nicrosini, M. Treccani
La Mappa Logistica è un modello matematico nato dal tentativo di spiegare l’evoluzione di una popolazione in ambiente con risorse limitate. La sua stilizzazione matematica è riassunta dalla semplice formula iterativa xn+1 = ? xn (1-xn).
Si noti che la legge matematica appena scritta è non lineare, contenendo nel membro di destra il quadrato della variabile. Nello studio della Mappa Logistica siamo interessati al valore assunto dalla variabile x dopo un grande numero di iterazioni (valore asintotico). Fissato un x iniziale tra 0 e 1, e calcolati gli x successivi, per valori di ? fino a 3 le iterazioni portano ad un unico valore asintotico (mostrato in figura)
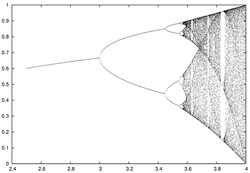
A partire da ?=3 insorgono nuove e sorprendenti caratteristiche.
Come si vede dalla figura ( sulle cui ascisse sono riportati i valori di ? e sulle cui ordinate sono riportati i valori asintotici ottenuti dall’iterazione della mappa) per ?=3 si realizza una biforcazione, nel senso che la mappa oscilla tra due valori, quelli mostrati in figura. Al crescere del valore di ? compaiono sempre nuove biforcazioni; la mappa oscilla tra un numero sempre maggiore di valori asintotici finché, per ?=3.57 il suo comportamento diviene per lo più caotico, con regioni di regolarità ancora presenti per alcuni valori di ?
La struttura del diagramma delle biforcazioni, noto come Albero di Feigenbaum, è frattale
[34] in corrispondenza delle biforcazioni, la mappa si auto-organizza oscillando tra un numero definito di valori, prima di divenire caotica.
Ma cos’è un frattale?