7. Un botanico, Einstein e la borsa

di G. Bormetti, C.M. Carloni Calame, G. Montagna, N. Moreni, O. Nicrosini, M. Treccani

Al giorno d’oggi non si conosce un modello matematico deterministico che descriva il comportamento dei mercati finanziari.

D’altra parte, la fenomenologia dei mercati finanziari esibisce caratteristiche simili a quelle trovate per la Mappa Logistica. Da un punto di vista “microscopico”, i mercati sono infatti costituiti da un insieme di persone ( "trader") ciascuno dei quali agisce in modo individuale e “relativamente semplice”. La complessità di questo sistema risiede nel fatto che dall’interazione di questi soggetti emergono effetti collettivi (ad esempio l’andamento dei prezzi delle azioni) non immediatamente riconducibili alle scelte operate dai singoli. Trovare una dinamica deterministica che descriva le scelte operate dai trader, non assicura quindi la prevedibilità a priori delle grandezze che sono significative per il sistema "mercato” considerato come un tutto.

Attualmente, le grandezze di mercato interessanti - come  il prezzo di uno strumento finanziario - vengono generalmente descritte da variabili stocastiche , ovvero che assumono valori casuali.

Ma cosa c’entra Einstein con i modelli che descrivono il comportamento della borsa?

Dobbiamo partire dai grani di polline…

1827-1905: alla Scoperta Del Moto Browniano

Nel 1827 il botanico inglese Robert Brown scoprì che grani di polline in sospensione acquosa si muovevano in modo frenetico seguendo traiettorie in apparenza “caotiche”. Lo stesso comportamento si poteva ottenere mettendo in sospensione altri tipi di corpuscoli purché le loro dimensioni fossero grandi rispetto a quelle delle molecole d’acqua.

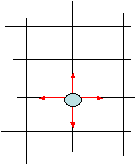
Nel 1905 Albert Einsteindiede un’interpretazione del fenomeno basata sull’esistenza di due livelli d’analisi: uno microscopico ed uno macroscopico. Al livello microscopico, troviamo il moto deterministico della particella mesoscopica (il grano di polline) regolato dall’equazione di Newton e  i cui cambiamenti repentini di direzione sono dovuti agli urti con le molecole d’acqua. Non potendo conoscere con precisione le condizioni iniziali, l’unico modo per modellizzare questo sistema è quello di passare ad un livello macroscopico. Si ipotizza così che l’effetto cumulativo degli urti porti la particella a muoversi in modo casuale, come se si trovasse su un reticolo e potesse saltare  da un sito all’altro con determinate probabilità.

Einstein ne derivò, per esempio, che la velocità quadratica media dovesse essere proporzionale alla Temperatura, come evidenziato dagli esperimenti di Brown.

l primo modello di Mercato Finanziario

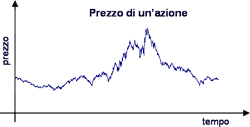
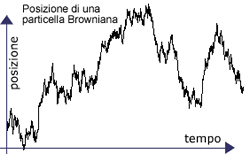
Strano a dirsi, nel 1901 Louis Bachelier , analizzò la variazione nel tempo dei prezzi dei titoli di Stato emessi dal governo francese e vide che avevano un andamento molto simile a quello della posizione di una particella unidimensionale “alla Brown”.

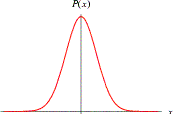
Propose così, senza conoscere il lavoro di Einstein, il primo modello “macroscopico” di mercato secondo il quale i prezzi delle azioni, risultanti da una serie di trattazioni di cui ignoriamo la dinamica microscopica, sono aleatori e la loro distribuzione di probabilità è la curva di Gauss o Gaussiana .

	Una densità di probabilità Gaussiana

Un Nobel per la Modellizzazione dei Mercati Finanziari

Nel corso degli anni si mostrò che il modello gaussiano di Bachelier non riproduceva in modo soddisfacente l’andamento dei prezzi e vari altri modelli vennero proposti. Quello che si configura ancora attualmente come modello “standard” per descrivere l’evoluzione dei prezzi delle azioni è il modello formulato nel 1973 da F. Black, M. Scholes e R. Merton per il quale Scholes e Merton sono stati insigniti del Premio Nobel per l’economia nel 1997 (Black è scomparso prematuramente nel 1995).

Le caratteristiche principali di questo modello sono: il logaritmo , del prezzo di un’azione si comporta come la posizione di una particella Browniana; ne segue che i prezzi hanno una distribuzione di probabilità “lognormale”; il prezzo di ogni prodotto finanziario soddisfa un’equazione del tipo “equazione differenziale alle derivate parziali”; in taluni casi esistono formule esplicite per calcolare questi prezzi. Formulata l’equazione di Black, Scholes e Merton mediante opportune variabili, è facile vedere che essa altro non è se non l’equazione di diffusione del calore!

Ecco un punto di contatto tra fisica e finanza! Questa equazione è quotidianamente utilizzata dagli operatori finanziari per definire il prezzo dei prodotti derivati da essi stessi venduti sul mercato.

Nasce l'econofisica .