percorso di Silvia Miozzi
Il limite per la costruzione di un ciclotrone è la dimensione del magnete.

Lawrence and staff at 184 inch Cyclotron ( LBL News Magazine)
Per ottenere energie elevate i magneti devono essere molto grandi, inoltre ad alte energie iniziano gli effetti relativistici, la velocità angolare non è più costante perché, secondo la relatività, la massa aumenta con la velocità, e le particelle vanno fuori fase con i campi acceleranti con la conseguenza che alla fine non c’è più accelerazione.
Per superare queste difficoltà nel 1944 il russo Vladimir Vekslerf propose l’idea del sincrotrone, progettato e costruito in modo indipendente nel 1945 dallo statunitense Edwin Mc Millan.
Questa macchina acceleratrice consiste di una camera da vuoto a forma di ciambella dentro la quale si fanno circolare le particelle che devono essere accelerate. Per compensare l’aumento di velocità e di massa i campi magnetici sono variabili nel tempo t, in modo che il raggio R dell’orbita rimanga costante
\[R=\frac{m(t)v(t)}{qB(t)}\]
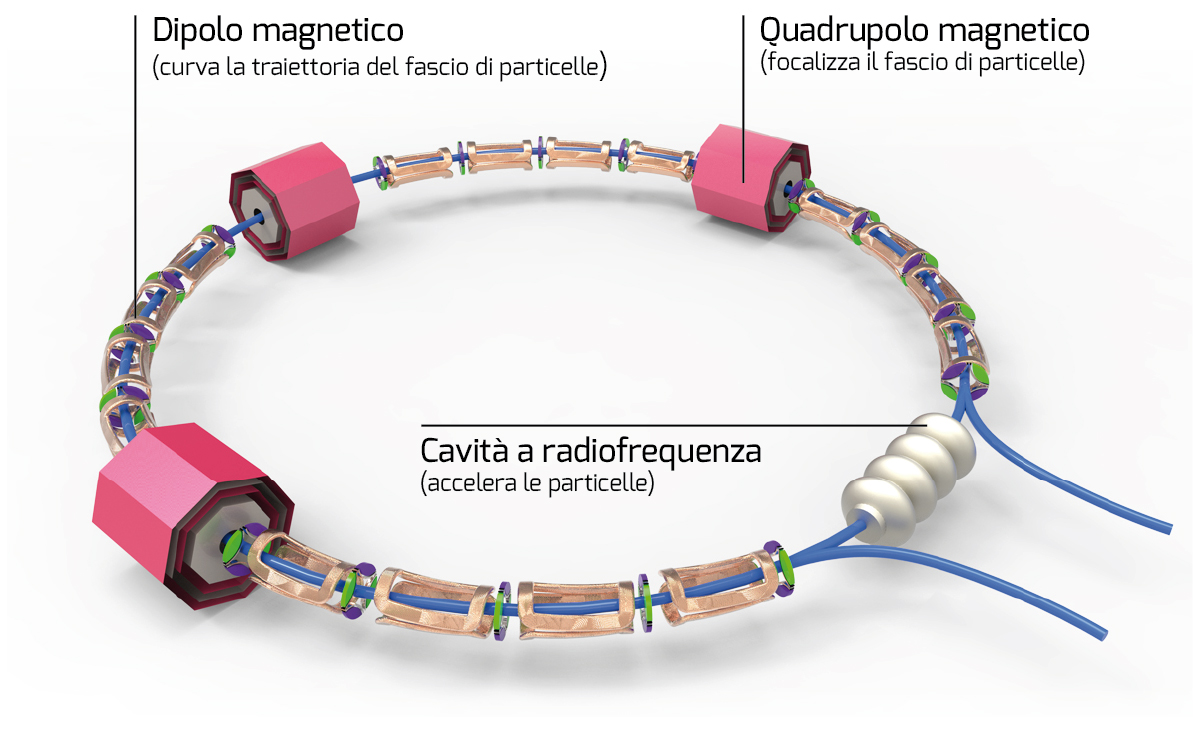
A differenza del ciclotrone, nel sincrotrone non c’è un unico grande magnete ma tanti piccoli magneti disposti lungo la traiettoria.
 (© Asimmetrie - F.Cuicchio)
(© Asimmetrie - F.Cuicchio)
Nella pratica le macchine di grande raggio vengono costruite a forma poligonale con sezioni dritte e spigoli arrotondati dove è presente un magnete per curvare la traiettoria. Le particelle acquistano energia nella cavità a radiofrequenza dove vengono accelerate, poi entrano in un susseguirsi di magneti curvanti e focalizzanti.
L'energia massima ottenibile da un acceleratore circolare è limitata dall'intensità dei campi magnetici e dal raggio massimo dell'orbita delle particelle.
Il limite di energia massima di un sincrotrone è dato quindi alla forza centripeta massima che i magneti riescono a fornire.
Per ottenere più energia è necessario avere magneti più potenti (possibile solo con la tecnologia dei superconduttori) oppure aumentare la dimensione del sincrotrone per avere curvatura minore, e quindi diminuire la forza centripeta necessaria.
L'energia massima ottenibile da un acceleratore circolare è limitata dall'intensità dei campi magnetici e dal raggio massimo dell'orbita delle particelle.
Il limite di energia massima di un sincrotrone è dato quindi alla forza centripeta massima che i magneti riescono a fornire.
|
Rigidità magnetica Possiamo calcolare l’aumento dell’impulso di una particella in funzione dell’intensità del campo magnetico e del raggio dell’acceleratore.
\[B=\frac{5,43\times 2700}{1232\times 14,3}=8,33 Tesla\] |

