percorso di Silvia Miozzi
Quando una particella incontra la sua antiparticella entrambe si annichilano rilasciando energia pura che si trasforma in nuove particelle in accordo con la legge E=mc2, dove E è l’energia alla quale avviene l’urto (la somma delle energie di particella e antiparticella), m è la massa totale delle particelle prodotte e c è la velocita della luce.
Negli anni ’50 del ‘900 fisici in varie parti del mondo ripresero un’idea di Wideroe che, durante la guerra, aveva immaginato di costruire dei collisori. Al tempo l’accelerazione di protoni (la particella più comunemente accelerata) non aveva ancora raggiunto i limiti relativistici. Quindi lo sforzo per costruire un acceleratore per scontrare fasci di protoni contro fasci di protoni, fu soprattutto intellettuale, ma gettò le basi per gli sviluppi dei decenni successivi.
Nel 1960 il fisico austriaco Bruno Touschek, che lavorava ai Laboratori Nazionali di Frascati dell’INFN, rivoluzionò completamente il concetto di bersaglio in un acceleratore pensando proprio alla possibilità di far collidere fasci di materia e antimateria.
Sfruttando gli stessi campi elettromagnetici è possibile accelerare, nello stesso anello, particelle in un verso e antiparticelle nel verso opposto e farle poi collidere in volo, in un punto ben definito. Il vantaggio di questa tecnica consiste nell’avere a disposizione dell’interazione la somma delle energie di particelle e antiparticelle che, annichilandosi, rilasciano tutta la loro energia per creare nuove particelle, mentre nel caso del bersaglio fisso la maggior parte dell’energia fornita alle particelle proiettili viene utilizzata per far muovere in avanti le particelle prodotte nell’urto.
 |
|
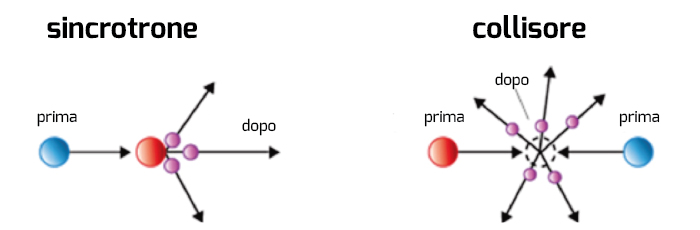| \[E_{CM}=\sqrt{2E_{beam}mc^{2}}\] | \[E_{CM}\approx 2E_{beam}\] |
Touschek progettò una macchina circolare che accelerava contemporaneamente in un verso elettroni e nell’altro positroni, le antiparticelle degli elettroni, in modo che i 2 fasci si incontrassero ad ogni giro e costruì un prototipo chiamato AdA (Anello di Accumulazione).
Sfruttando questa idea sono stati costruiti quasi tutti i principali collisori degli ultimi decenni. Nel campo degli apparati che producono scontri di elettroni contro positroni, il più grande finora costruito è stato il LEP (Large Electron Positron) collisore al CERN. Nel tunnel del LEP è stato installato l'LHC, dove si scontrano fasci di protoni che circolano in direzioni opposte. Nel passato due collisori (uno al CERN e uno a Fermilab negli USA) hanno effettuato collisioni di protoni con antiprotoni.
|
Massa invariante e sistemi di riferimento Consideriamo un insieme di N particelle ognuna con quadrimpulso \(P_k = [E_k/c ~; p_k]\). Il quadrimpulso totale \(P_{tot} = \sum P_k\). La quantità invariante \[\sqrt{s}=\sqrt{c^{2}P_{tot}^{2}}=\sqrt{(\Sigma E_{k})^{2}-(\Sigma p_{k})^{2}c^{2}}=E_{CM}\] è denominata massa invariante del sistema o energia nel centro di massa. Sistema di riferimento del laboratorio Consideriamo una particella che incide su un bersaglio, nel quale quindi la particella interagente del bersaglio è ferma rispetto al sistema di riferimento del laboratorio. I rispettivi quadrimpulsi sono \(P_1=[E_1 /c~; p_1]~~~~~P_2=[m_2 c~;0]\) Il quadrimpulso totale è \(P_{tot}=[E_1/c~+~m_2 c~; p_1]\) La massa invariante è \[\sqrt{s}=\sqrt{(E_{1}+E_{2})^{2}-(p_{1}+p_{2})^{2}c^{2}}=\] \[=\sqrt{(E_{1}+m_{2}c^{2})^{2}-p_{1}^{2}c^{2}}=\] \[=\sqrt{m_{1}^{2}c^{4}+m_{2}^{2}c^{4}+2E_{1}m_{2}c^{2}}\] Per particelle ultrarelativistiche per le quali la massa può essere trascurata \[E_{CM}=\sqrt{2E_{1}mc^{2}}\] Sistema di riferimento del centro di massa Consideriamo 2 particelle di massa identica che viaggiano alla stessa velocità ma in versi opposti \[P_1=[E_1/c~;~p_1];~~~P_2=[E_2/c~;~p_2];~~~E_1=E_2;~~~p_1=-p_2\] \[E_{CM}=\sqrt{s}=2E\] |
