di G. Bormetti, C.M. Carloni Calame, G. Montagna, N. Moreni, O. Nicrosini, M. Treccani

Nello studio dei fenomeni fisici si possono evidenziare due situazioni dinamiche estreme.

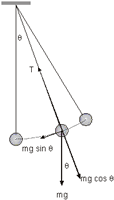
Nella prima di queste, il sistema sotto osservazione evolve in modo completamente prevedibile. Un esempio molto noto di tale sistema è il pendolo semplice in regime di piccole oscillazioni. In questo caso, la forza che richiama il pendolo alla posizione di equilibrio è proporzionale allo spostamento. L’equazione del moto in tale situazione è lineare nella variabile incognita, e questo garantisce la completa prevedibilità del moto. All’estremo opposto si collocano quei sistemi fisici che, pur governati da una dinamica deterministica , si comportano in modo di fatto imprevedibile: sono i cosiddetti sistemi caotici, il cui comportamento sembra estraneo a qualunque legge deterministica di fondo. Un esempio paradigmatico di tali sistemi è il cosiddetto pendolo caotico.

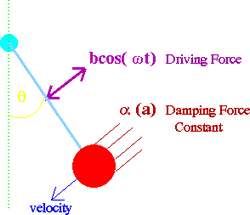Si tratta di un pendolo simile a quello dell’esempio precedente, ma libero di oscillare con ampiezza arbitraria. Esso, inoltre, è soggetto sia all’azione dell’attrito che all’azione di una forza esterna sinusoidale, caratterizzata da una certa ampiezza e una data frequenza. In tale situazione, la forza cui è soggetto il pendolo non è più proporzionale allo spostamento. L’equazione del moto è non lineare, gli effetti non lineari sono importanti e fanno sì che per certi valori di ampiezza e frequenza della forza esterna il pendolo sia animato da moto caotico, cioè da moto criticamente dipendente dalle condizioni iniziali.

Questa forte dipendenza rende di fatto imprevedibile l’evoluzione nel tempo del sistema: è per esempio sufficiente far partire il pendolo da posizioni impercettibilmente diverse per ottenere evoluzioni nel tempo completamente differenti.

Cosa c’entra la complessità con tutto questo?

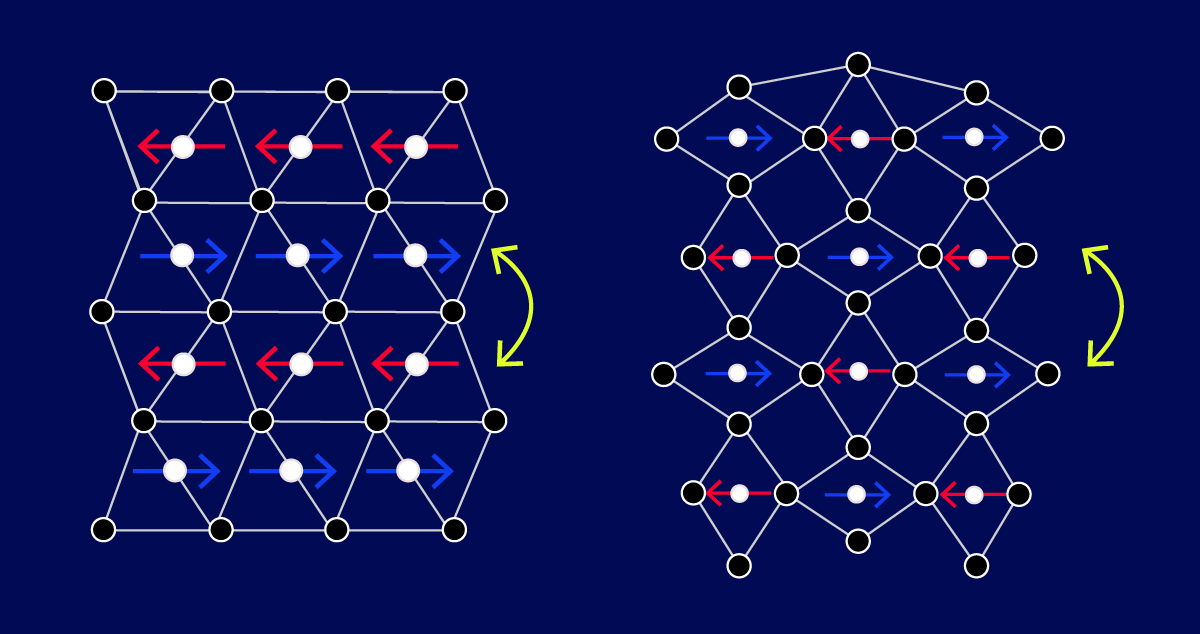
Ebbene, esistono sistemi che possono venire a trovarsi, al variare delle condizioni cui sono sottoposti, in una situazione dinamica intermedia tra quella completamente prevedibile del primo esempio e quella caotica e imprevedibile del secondo. In tale situazione il sistema manifesta proprietà “emergenti”: al confine tra ordine e caos si assiste all’apparizione improvvisa (emergence) di regolarità inattese, come l’auto-organizzazione: questo comportamento, molto particolare, rappresenta una possibile definizione di complessità. Esistono, e ne vedremo esempi, sistemi complessi sia nella natura che nella società. Iniziamo ad occuparci di un modello matematico che presenta tutte le caratteristiche di complessità appena discusse.