percorso di Marco Capogni
All’epoca di Planck si conoscevano dunque le seguenti costanti della natura:
-la costante di gravità, \(G\), introdotta da Newton;
-la velocità della luce nel vuoto, \(c\), misurata e deducibile dalle equazioni di Maxwell;
-il quanto di azione \(h\) di Planck.
Fu proprio Planck, riflettendo sulle tre costanti universali, a notare che esse potevano essere combinate tra di loro per ricavare un valore di:
massa \(m_P=\sqrt{ħc/G}\), nota come massa di Planck e pari a circa \(10^{-8} kg\);
lunghezza \(l_P=\sqrt{ħG/c^3 }\), nota come lunghezza di Planck e pari a circa \(10^{-35} m\);
tempo \(t_P=l_P/c=\sqrt{ħG/c^5}\), noto come tempo di Planck e pari a circa \(10^{-44} s\).
Le tre grandezze \(m_p\), \(l_p\) e \(t_p\), apparvero subito come “unità” di misura naturali di massa, lunghezza e tempo, costituendo così un sistema metrologico fondamentale e pertanto chiamate “unità di Planck” o “unità naturali” o “unità assolute”. Rispetto ad esse, \(G=c=ħ=1\) e la carica dell’elettrone e del protone risulta essere approssimativamente \(e=1/√137\), dove \(137\) è circa il reciproco della costante di struttura fine ( \(\alpha = e^2/ħc\) ), che regge l’intensità delle interazioni elettromagnetiche e che ritroviamo naturalmente nella teoria atomica di Bohr, dove la forza di Coulomb tra elettrone e protone è combinata con l’ipotesi del ‘quanto di azione’ di Planck.
Il significato fisico delle unità di Planck iniziò a chiarirsi solo con gli sviluppi della teoria della relatività generale in relazione alla meccanica quantistica. Se si è riusciti a far comunicare relatività ristretta e meccanica quantistica in modo mirabile nella elettrodinamica quantistica, diversamente il tentativo di mettere insieme la relatività generale - una teoria sviluppata specialmente per dar ragione a fenomeni su scale cosmiche - e la meccanica quantistica - teoria che descrive mirabilmente il mondo microscopico - fu pieno di ostacoli, e ad oggi non esiste una visione completa di piena convergenza tra le due, come di seguito discusso.
 |
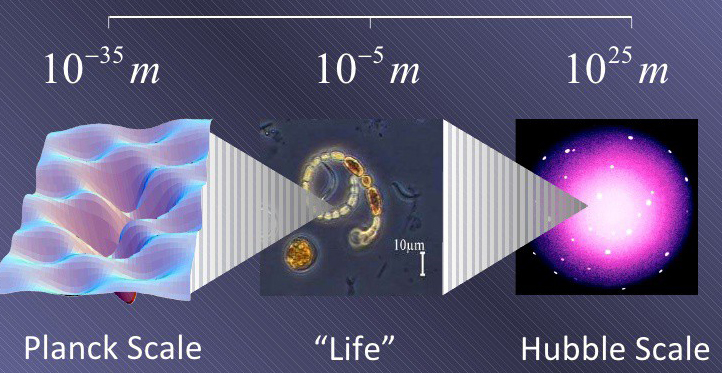 |
| fig. 25, lunghezza di Planck (lp) |
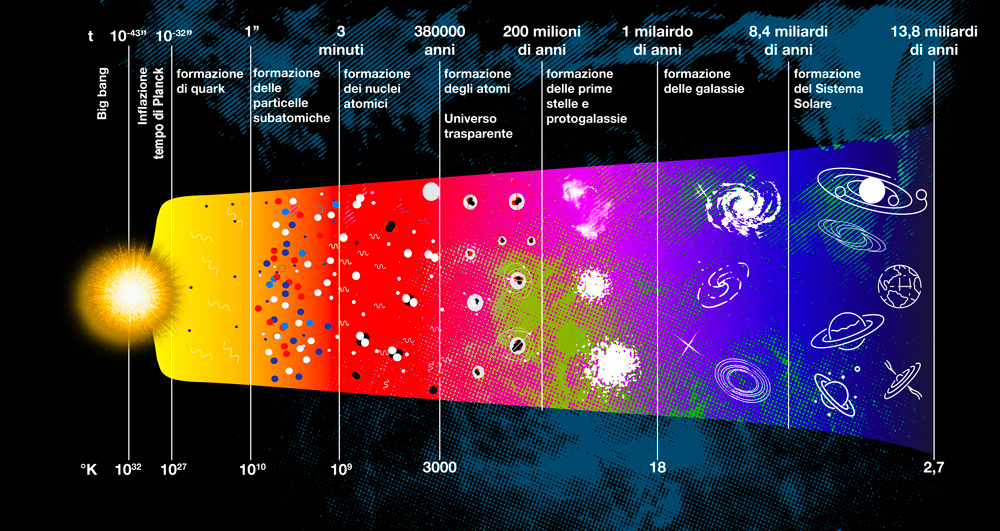
fig. 26, Tempo di Planck (tp)

