percorso di Marco Capogni
La perdita in meccanica quantistica della descrizione nel contempo spazio-temporale e causale dei fenomeni (e quindi l’inadeguatezza delle forme di linguaggio proprie della fisica classica, che via via si delineavano nello studio dell’atomo), portò a una nuova struttura matematica della natura, che per i fenomeni quantum-meccanici sembrava non aver più bisogno nemmeno delle forme geometriche del mondo di Galileo, Newton, Maxwell ed Einstein, proprio per l’incapacità di descrivere la traiettoria di un’onda-corpuscolo.
La nuova struttura matematica che fu proposta per descrivere l’atomo di Bohr si basò, in modo equivalente sulla:
- teoria della funzione d’onda \(Ψ\) (Fig. 14), introdotta da Erwin Schrӧdinger (Vienna, 1887 – 1961), che consente di descrivere gli stati stazionari dell’atomo ipotizzati da Bohr;
- teoria delle matrici, sviluppata da Heisenberg, rappresentanti osservabili fisiche (come l’energia \(H\) di un sistema meccanico), che consentono di descrivere i ‘salti quantici’ degli elettroni nell’atomo tra gli stati stazionari.
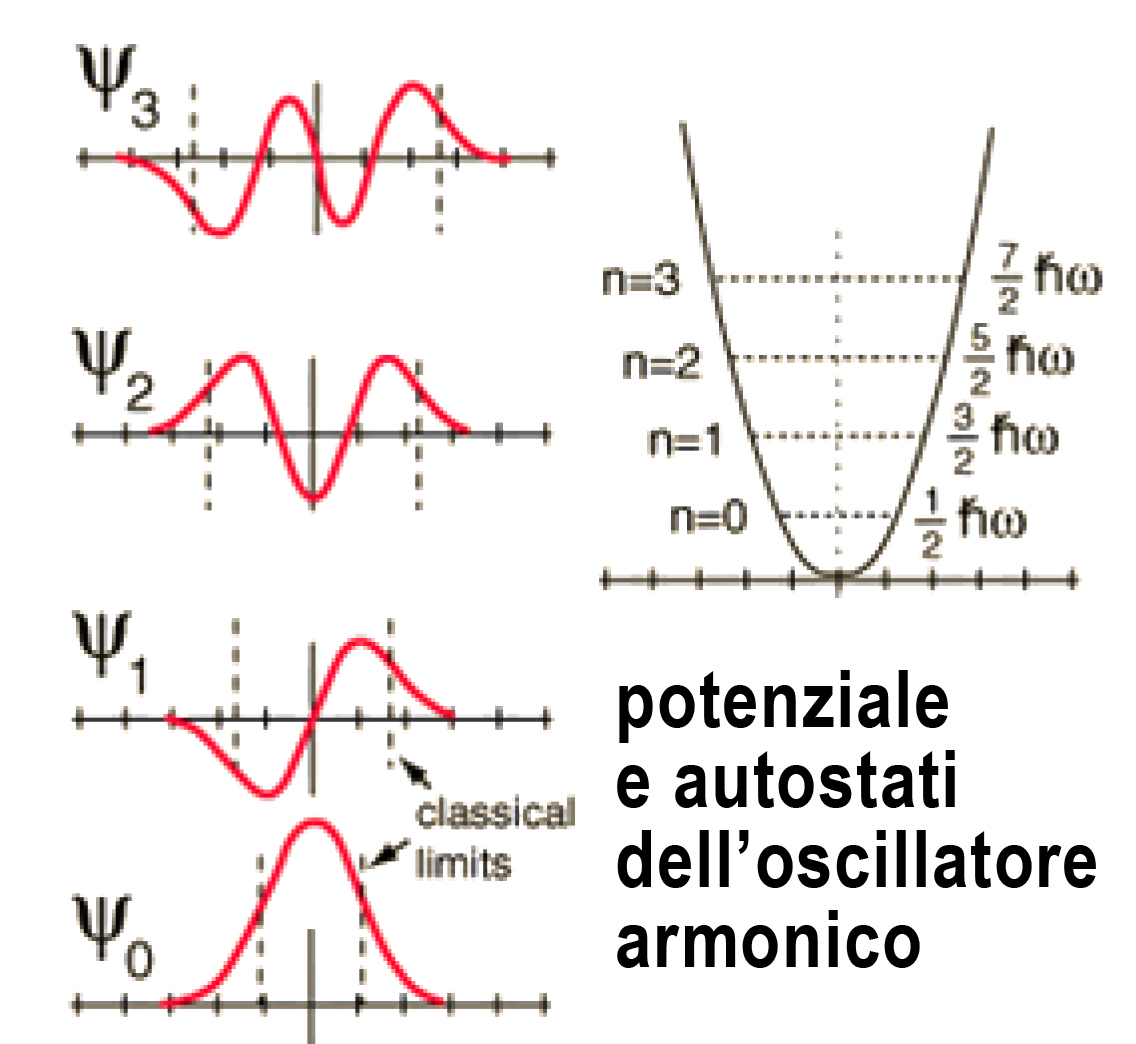
In tale nuova struttura della meccanica quantistica (considerando ad esempio il caso dell’oscillatore armonico con pulsazione \(\omega\)), gli stati stazionari corrispondono - nella rappresentazione di Schrӧdinger - a determinate configurazioni, \(Ψ_0, Ψ_1, Ψ_2, Ψ_3, …, Ψ_n, …., \) della funzione d’onda \(Ψ\) per determinati valori \(E_n=(n+1/2)ħ \omega \) di energia. Tali valori di \(E_n\) sono - nella rappresentazione di Heisenberg - i valori diagonali di una matrice infinito-dimensionale; l’insieme di questi costituisce il suo ‘spettro di autovalori’ associati ai suoi autostati, che a loro volta corrispondono alle \(Ψ_n\).
 |
 |
| fig. 14: Energia \(H\) e funzioni d’onda \(Ψ\) dell’oscillatore armonico (rappresentazione di Schrӧdinger) | fig. 15, Energia \(H\) dell’oscillatore armonico (rappresentazione di Heisenberg) |
Entrambe le rappresentazioni ovviamente non trovano un loro analogo riscontro nella fisica classica e sono prettamente tipiche della meccanica quantistica e del mondo microscopico che essa descrive. L’insieme di autostati e autovalori di matrici infinito-dimensionali, come quella indicata in Fig.15, associate ad osservabili fisiche - quale l’energia \(H\) di un sistema meccanico o l’impulso \(p\) o la posizione \(q\) di un’onda-corpuscolo -, troverà una sua naturale collocazione nello spazio di Hilbert, che svolgerà nella meccanica quantistica il ruolo svolto dallo spazio delle fasi nella fisica classica.

