percorso di Marco Capogni
Assumendo dunque valida l’ipotesi di de Broglie di considerare la duplice natura ondulatoria e corpuscolare anche per le particelle materiali, come gli elettroni, e non solo per quelle di luce, come i fotoni, si evidenziò subito l’inadeguatezza dell’apparato matematico della fisica classica per descrivere questo nuovo oggetto della realtà costituito dall’onda-corpuscolo.
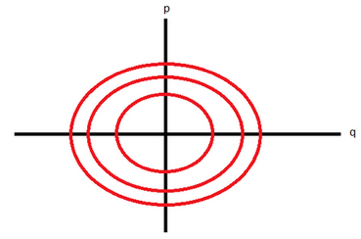
Un potente strumento matematico della fisica di Newton e di Maxwell è infatti rappresentato dallo spazio delle fasi, individuato dalle coordinate spaziali \(q\) e gli impulsi \(p\) di un sistema di particelle. La relazione a istanti temporali diversi delle coppie di variabili \(q\) e \(p\) definisce nello spazio delle fasi una traiettoria di fase, come in Fig. 10 in cui sono rappresentate, in rosso, le traiettorie di fase per un oscillatore armonico di costante elastica \(\kappa\), massa \(m\) e pulsazione \(\omega=\sqrt{\kappa/m}\) per diversi valori dell’energia meccanica \(H\) data dalla somma dell’energia cinetica \(K=K(p)=p^2/2m\) e potenziale \(U=U(q)=kq^2/2\), \(H=H(q,p)=K(p)+U(q)\) e pari a:
\[H(q,p)=\frac{p^2}{2m}+ \kappa \frac{q^2}{2} ~(5)\]
che costituisce una funzione, o meglio un funzionale, che da coppie di valori \( (q,p) \) restituisce una quantità scalare e le cui curve di livello, date da valori costanti di \(H\), sono proprio le traiettorie di fase sul piano \( (q,p) \).
 |
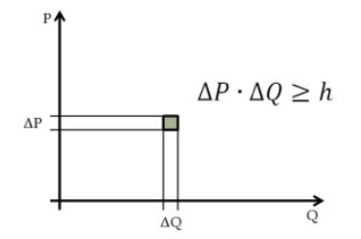 |
| fig. 10, Spazio delle fasi di un oscillatore armonico in Fisica Classica | fig. 11, Spazio delle fasi in Meccanica Quantistica |
Nello spazio delle fasi si può definire anche un’ulteriore grandezza scalare, ovvero un ulteriore funzionale, data dal prodotto \(p·q\) misurato sui cammini di fase, più precisamente dato dall’espressione matematica di integrale sulla traiettoria di fase e definito da \(A = ∫_{q_1}^{q_2}pdq\). Tale grandezza, che rappresenta un’area sottesa da una determinata curva di fase tra due posizioni \(q_1\) e \(q_2\) nel piano \((p,q) \), ha le dimensioni di un’energia per un tempo e a cui si dà il nome di azione. Essa può essere definita in termini di integrale su una traiettoria di fase se e solo se vige il principio di differenziabilità di tale traiettoria, sicuramente valido per i sistemi fisici classici secondo l’ipotesi implicita nella fisica classica che tutte le grandezze misurabili possono variare in modo continuo e assumere qualsiasi valore compatibilmente con le condizioni del fenomeno studiato. Rappresentando l’azione in termini dell’energia cinetica \(K\) del sistema per un moto nello spazio fisico tra due istanti temporali \(t_1\) e \(t_2\), si ha \( A = ∫_{t_1}^{t_2}2Kdt \). Da questa definizione si ha che, per i sistemi identificati da un funzionale \(H(q,p)\) (noto tecnicamente anche come hamiltoniana del sistema fisico), come ad esempio in equazione (5), la circuitazione di \(A \) su una traiettoria di fase chiusa (Fig.10), matematicamente scrivibile come \( I = \oint p dq\), è stazionaria ovvero costante nel tempo e nota come invariante di Poincaré. Il concetto di azione trovò un fecondo sviluppo nella fisica iniziata con Galileo e Newton. Infatti, per sistemi conservativi, che ammettono un’energia potenziale \(U(q)\), l’inclusione di tale funzione nella definizione di \(A\) portò alla definizione dell’azione hamiltoniana \(S\) data da \(S= ∫_{t_1}^{t_2}(K-U)dt\), dove \(L = K - U\) è un nuovo funzionale dello spazio delle fasi, chiamato lagrangiana del sistema fisico considerato. In tutta la fisica classica vale un principio fondamentale, noto come principio variazionale di Hamilton, per cui per un sistema conservativo il moto del sistema avviene in modo da rendere minima \(S\). Tale principio, conosciuto anche come ‘principio di minima azione’, permette di ricavare, una volta definita la lagrangiana \(L\), tutte le equazioni della fisica di Newton, di Maxwell e della teoria della relatività. Si comprende bene allora la preoccupazione di Planck nel pensare al suo ‘quanto elementare di azione’ e all’imponente edificio della fisica classica e della teoria della relatività, costruito e fondato sul principio variazionale di Hamilton. Come riporta lo stesso Bohr [9], nel primo congresso di Solvay - “Teoria della radiazione e quanti” (1911) - Planck, nel presentare il nuovo schema concettuale che si stava delineando con il ‘quanto di azione’, mise in evidenza che: “il punto essenziale non era tanto l’introduzione della nuova ipotesi dei quanti di energia, quanto il rimodellamento del concetto stesso di azione”.
Nella fisica classica, infatti, compatibilmente con le energie in gioco nel particolare sistema meccanico o elettromagnetico considerato e con il valore del funzionale di azione, tutti i punti dello spazio delle fasi \((q,p)\) sono in linea di principio ammissibili. Diversamente in meccanica quantistica l’equazione (4) evidenzia che per l’onda-corpuscolo esiste una relazione di coniugio tra la coordinata spaziale \(q\), individuata dal valore di \(\lambda\), e l’impulso \(p\), per cui se \(\Delta q\) è un intervallo spaziale in cui trovare l’onda-corpuscolo, e \(\Delta p\) è l’incertezza sul valore dell’impulso coniugato, la (4) comporta che \(\Delta q\cdot \Delta p \ge h\), che è, a parte una costante pari a \(1/4\pi\), l’espressione matematica del principio di indeterminazione di Heisenberg.
Tale principio sta quindi ad indicare che in meccanica quantistica l’area dello spazio delle fasi (Fig. 11) è inferiormente limitata dal ‘quanto di azione’ di Planck. In altri termini l’esistenza del quanto ha come effetto quello di rendere discreto ovvero granulare anche lo spazio delle fasi, facendo cadere così la proprietà di differenziabilità della traiettoria di fase, su cui si basa la definizione delle equazioni del moto ricavate dal principio di minima azione. Ovviamente tutto ciò ebbe una forte implicazione sulla struttura matematica della nuova teoria perché la rappresentazione classica delle traiettorie, sia nello spazio fisico sia in quello delle fasi, tipica della fisica classica non poteva più valere per oggetti quantistici come l’onda-corpuscolo. Si presentò dunque già dall’inizio la necessità di trovare una nuova matematica adatta alla descrizione dei fenomeni quantistici; tale necessità si rese ancora più palese nel momento in cui si studiarono a fondo le problematiche degli spettri di emissione e assorbimento degli atomi e si cercò di fornire un quadro coerente ai concetti degli ‘stati stazionari’ introdotti da Bohr.

