percorso di Marco Capogni
Sempre sulla base del principio di indeterminazione di Heisenberg, è chiaro che nel mondo microscopico - così come intrepretato dalla meccanica quantistica, in cui gli effetti del quanto di azione di Planck non sono trascurabili - la descrizione “causale”, che Bohr considera basata sulle leggi di conservazione di energia e momento [10], propria del determinismo classico e strettamente connessa alla struttura spazio-temporale della fisica classica, non è difatti più valida. Bohr, che comprende a fondo la rivoluzione introdotta nella fisica e quindi nella natura dal ‘quanto di azione’ di Planck, mette in luce che la rappresentazione del mondo atomico, basata sulla sua ipotesi degli stati stazionari per gli elettroni nell’atomo, non consente di realizzare mentalmente un modello spazio-temporale di tale sistema secondo i canoni della fisica di Galileo e Newton. Afferma testualmente Bohr che:“[…] qualsiasi tentativo di fissare le coordinate spazio-temporali delle particelle costituenti di un atomo comporterebbe alla fine uno scambio incontrollabile di energia e momento con i regoli e gli orologi […]. Viceversa, ogni applicazione dei teoremi di conservazione, per esempio del bilancio energetico nelle reazioni atomiche, comporta una rinuncia essenziale riguardo all’individuazione nello spazio e nel tempo delle particelle atomiche individuali. In altre parole, l’uso dell’idea di stati stazionari sta in una relazione di mutua esclusione con l’applicabilità di rappresentazioni spaziotemporali”[11].
L’esistenza di stati stazionari nell’atomo e la possibilità del ‘salto quantico’ tra uno stato e l’altro da parte di un elettrone atomico con emissione di un fotone (Fig. 12), si giustifica, nell’ambito della rappresentazione di Bohr, ipotizzando che, non solo l’energia del fotone (che viene emesso o assorbito) è quantizzata secondo la regola di Planck, ma lo è anche il momento angolare orbitale \(\vec{M}\) dell’elettrone. Questo è dato dal prodotto vettoriale (\(\times\)) tra il raggio vettore \(\vec{r}\) di tale elettrone e la sua quantità di moto \(\vec{p}=m\vec{v}\) e quindi espresso come \(\vec{M} = \vec{r} \times \vec{p}\).
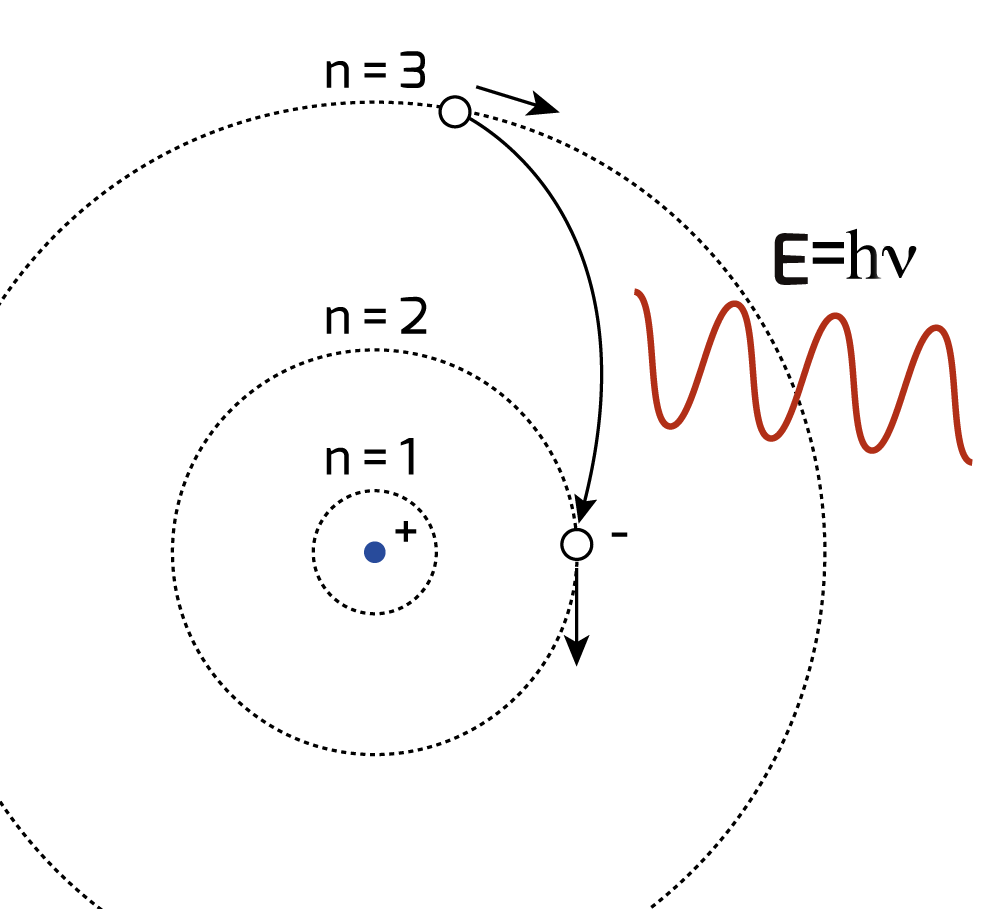 |
fig. 12, Il salto quantico dell’elettrone tra stati stazionari dell’atomo con emissione o assorbimento di un fotone (ipotesi di Bohr) |
Più specificatamente per gli elettroni sugli stati stazionari dell’atomo (pensati orbitare intorno al nucleo in modo circolare per cui \(M= r·p=r·mv\) ) vale la regola di quantizzazione di Bohr:
\[M= nħ ~(6)\]
dove \(ħ=h/2π\) è la costante ridotta di Planck e \(n=1, 2, 3.. \) è il numero quantico principale che individua l’orbitale corrispondente al determinato valore di \(n\) e dunque di \(M\). L’espressione (6) evidenzia proprio che sugli stati stazionari di Bohr l’invariante di Poincaré nello spazio delle fasi \(I=\oint pdq\) pari a \(p·2πr\) coincide - in questo caso particolare e a parte un fattore \(2\pi\) - con il valore scalare del momento angolare \(M\) del sistema atomico nello spazio fisico; esso risulta quantizzato in unità elementari della costante di Planck (o quanto elementare di azione). E’ questo il primo vero gradino nella teoria della conoscenza del mondo atomico, che verrà sviluppata e consolidata negli anni successivi.
La regola di Bohr, che costituisce la base della prima descrizione quantum-meccanica dell’atomo, produce una dipendenza dell’energia meccanica \(E_n\) dell’elettrone, circolante su un determinato orbitale, dal numero quantico \(n\); ciò permette di giustificare, con l’ammissione dell’esistenza del ‘salto quantico’ tra stati stazionari dell’atomo, gli spettri discreti di assorbimento ed emissione osservati (Fig. 13). Tale regola evidenzia anche che a livello microscopico le varie grandezze meccaniche \(E, M, .. \) sono di fatto discontinue.
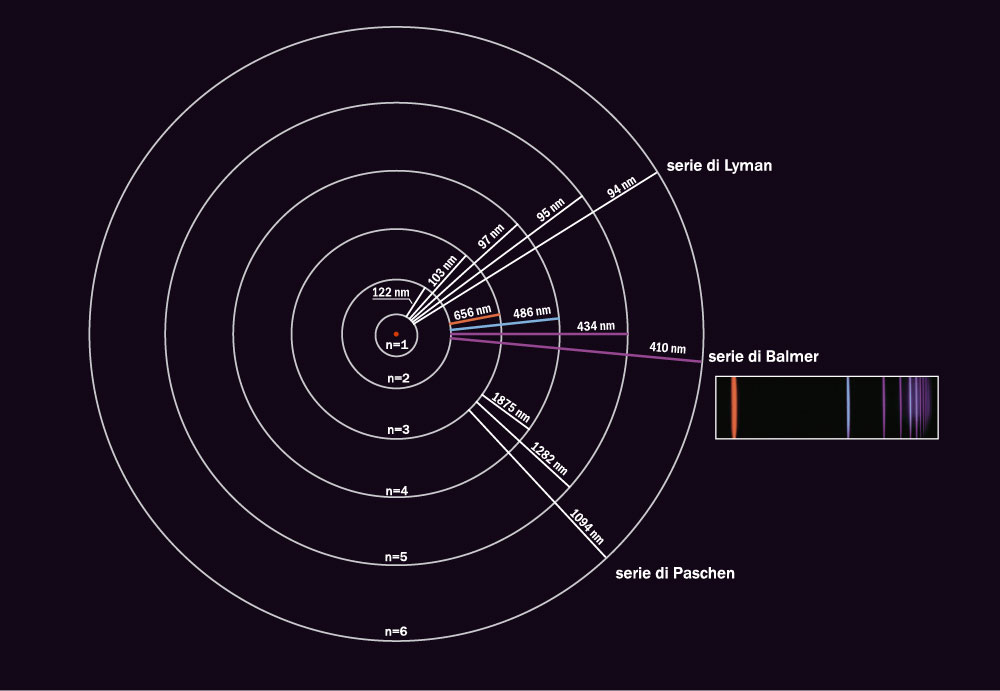
fig. 13, Spettro dell’atomo di Idrogeno
Uno sviluppo successivo della teoria di Bohr, dovuto ad Arnold Sommerfeld (Kӧnigsberg, 1868 – Monaco di Baviera, 1951), portò a definire gli orbitali elettronici non solo in termini del numero quantico \(n\) ma anche di altri due numeri quantici \(l \) (numero quantico orbitale), con \(0≤l≤n-1\), e \(m_l\) (numero quantico magnetico), con \(-l≤m_l≤l \), entrambi associati a \(M\) e tali da fornire indicazioni sull’eccentricità dell’orbitale e sulla sua orientazione nello spazio. Tuttavia, in questa descrizione di Bohr-Sommerfeld dell’atomo, si nota ancora il forte legame con schemi e modelli (vettori, orbite, etc.), anche geometrici, tipici della fisica classica. Fu proprio Ernest Rutherford (Brightwater, 1871 – Cambridge, 1937) ad evidenziare questo fatto nel rispondere con una lettera datata 20 Marzo 1913 a Bohr (che gli aveva sottoposto il suo lavoro sulla struttura dell’atomo). Di seguito le testuali parole della lettera: <Caro dottor Bohr, […] Le Sue idee sull’origine dello spettro dell’idrogeno sono molto ingegnose e sembrano funzionare bene; ma la mescolanza delle idee di Planck con la vecchia meccanica consente molto difficilmente di formarsi un’idea fisica della base di tutto il discorso[…]> [9]. Ben presto infatti la rappresentazione di Bohr-Sommerfield dell’atomo venne abbandonata a favore di una nuova e più appropriata descrizione del mondo quantistico.

