9. I paradossi del mondo quantistico

percorso di Marco Capogni

La meccanica quantistica, allontanandosi sempre più dalla struttura della fisica classica, portò inevitabilmente anche a scontrarsi con situazioni paradossali dovute, come Bohr e Heisenberg continuamente hanno sottolineato nei loro scritti, a una mancanza di un vero e proprio linguaggio adeguato alla nuova situazione fisica.
Già Rutherford nella sua lettera a Bohr (precedentemente citata) mise in risalto che c’era qualcosa di anomalo nella nuova teoria dell’atomo presentatagli dallo scienziato danese. Prosegue Rutherford nella lettera: “Mi sembra ci sia una grave difficoltà nelle Sue ipotesi, che non penso affatto Le sia sfuggita: come fa un elettrone a decidere con quale frequenza deve vibrare quando passa da uno stato stazionario all’altro? Sembra che si debba supporre che l’elettrone sappia in partenza dove andrà a finire.”[9].
La situazione, sebbene si complicò da un punto di vista matematico, iniziò comunque a chiarirsi con gli sviluppi della teoria quantistica di Schrӧdinger e Heisenberg, descritti in precedenza. Le matrici di Heisenberg, pur rappresentando grandezze fisiche (come posizione \(q\), impulso \(p\), energia \(E\), momento angolare \(M\), etc.), mostravano una natura particolare per proprie regole algebriche che evidenziavano relazioni di anti-commutazione per alcune variabili coniugate (come \(q\) e \(p\)). Ciò portò, nella nuova struttura matematica ideata, ad una rappresentazione elegante del principio di indeterminazione; esso infatti viene spiegato dal fatto che il commutatore tra \(q\) e \(p\) - inteso come \((qp-pq)=[q,p] \) dove \(q\) e \(p\) sono ora matrici infinito-dimensionali nello spazio di Hilbert - non è nullo bensì pari a \(iħ\). Le onde di Schrӧdinger, pensate inizialmente alla maniera di de Broglie come onde pilota per la particella quantistica, sembravano fornire invece (secondo quella che fu chiamata interpretazione di Bohr-Born) un’ampiezza di probabilità di trovare in una determinata regione spaziale l’onda-corpuscolo definito dall’equazione (4).
Ovviamente tutto questo nuovo apparato matematico non sembrava fornire una rappresentazione della <realtà>, bensì un formalismo tale da consentire di <computare probabilità per realtà alternative che potrebbero avvenire>[12], dando così luogo ad un’ontologia quantistica nota come ‘spirito di Copenaghen’ (Kopenhagener Geist), di cui Bohr e Heisenberg furono i principali sostenitori.

Il processo di misura

Un aspetto particolare di questa interpretazione della meccanica quantistica è rappresentato dal paradosso della misura: esiste infatti in essa una profonda problematica del rapporto tra il soggetto, che esegue la misura, e l’oggetto, che la subisce. Nella fisica classica la distinzione tra soggetto e oggetto era netta e ben definita. Ciò consentiva di affermare che la realtà poteva essere ben conosciuta con il processo di misura e che una non completa conoscenza del sistema fisico era essenzialmente dovuta a una cattiva risoluzione dello strumento impiegato.

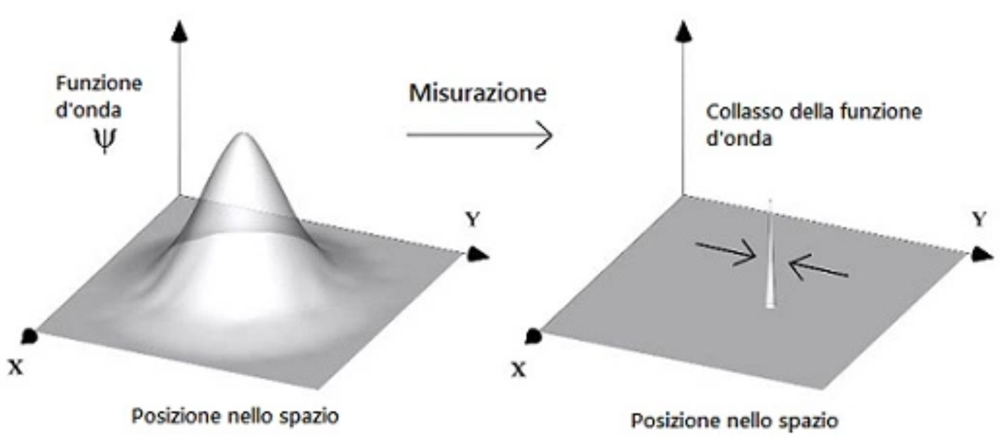fig. 16, collasso della funzione d’onda

 In meccanica quantistica la situazione è ben differente. La funzione d’onda \(Ψ\) obbedisce all’equazione d’onda di Schrӧdinger che è essenzialmente lineare, continua e deterministica nello spazio e nel tempo. Il processo di misura, che individua un ben preciso valore di un osservabile fisico (quale la posizione dell’onda-corpuscolo nello spazio), produce quello che viene chiamato collasso della funzione d’onda (Fig. 16), noto anche come “riduzione dello stato quantico”[12]. Tale processo presenta una natura discontinua e probabilistica e fa perdere qualunque informazione di causa ed effetto (e quindi connessione tra passato e futuro) esistente invece per la \(Ψ\).

Il gatto di Schrӧdinger

L’applicazione dei principi della meccanica quantistica a stati macroscopici - ovvero lontani dai valori del quanto elementare di azione di Planck - porta a situazioni paradossali, come evidenziò lo stesso Schrӧdinger in un celeberrimo esperimento mentale ideato nel 1935 e noto appunto come ‘gatto di Schrӧdinger’ (Fig. 17). La natura probabilistica della funzione d’onda e la linearità della equazione d’onda, che essa soddisfa, implica che un gatto chiuso in una scatola con una fiala di cianuro, che può essere rotta da un martelletto azionato da una sostanza radioattiva, è rappresentato da una funzione \(Ψ\) dell’intero sistema tale che la situazione ‘gatto vivo’ e ‘gatto morto’ non sono stati puri ma miscelati in uno stato di sovrapposizione con ugual peso, per cui è come se il gatto fosse contemporaneamente vivo e morto.

fig. 17, il gatto di Schrӧdinger

L’entanglement

L’ontologia quantistica convenzionale rappresentata dallo ‘spirito di Copenaghen’ non è l’unica esistente della meccanica quantistica, ma ne esistono ben sei diverse alternative [12]. All’interpretazione di Bohr e Heisenberg della nuova teoria dell’atomo (per le conseguenze che essa portava sia nella struttura conoscitiva del mondo sia nella idea stessa di realtà), furono mosse accese critiche da diversi fisici loro contemporanei. Einstein infatti mai accettò, quale fondamento della natura, l’idea dell’indeterminazione quantistica, con tutto l’aspetto probabilistico che essa conteneva alla sua base. Egli arrivò a pensare che la meccanica quantistica fosse una teoria incompleta.

Fig. 18: entanglement quantistico

Nonostante la teoria sembrasse funzionare bene per descrivere il mondo degli atomi, conteneva secondo Einstein delle contraddizioni di fondo, che egli mise in evidenza con il paradosso EPR (Einstein-Podolsky-Rosen) [13]. Il meccanismo EPR è un esperimento mentale che riesce a prevedere il fenomeno dell’entanglement quantistico, conseguenza dei postulati della meccanica quantistica ; tale fenomeno porta all’esistenza di stati/particelle accoppiati (anche se fisicamente distanti e in linea di principio non influenzabili a vicenda), a causa della natura ‘olistica’ – cioè definita contemporaneamente su tutto lo spazio fisico - della funzione d’onda [12]. Tale proprietà viola un principio che Einstein considerava fondamento di tutte le teorie della fisica: il ‘principio di località’. Sulla base della costanza e finitezza della velocità della luce nel vuoto (che a sua volta elimina il concetto di azione a distanza di Newton) tale principio stabilisce che, oggetti distanti non possono avere influenza istantanea l’uno sull’altro.

La bizzarria dell’entanglement, fenomeno totalmente e unicamente quantistico come gli altri due precedentemente esaminati, fa si che qualcosa che accade in un posto può influenzare istantaneamente qualcos’altro che accade altrove, introducendo di nuovo nella fisica - come disse Einstein - una ‘sinistra azione a distanza’. Sul paradosso EPR intervenne Bohr, che formulò una sua difesa della meccanica quantistica non accettata da diversi eminenti fisici impegnati sul problema, che quindi rimase irrisolto. In questo caso comunque i fatti storici che seguirono hanno dato ragione alla meccanica quantistica [14].
Una domanda resta, tuttavia, ancora aperta: “perché le particelle sono entangled?“. Forse come affermato in [15] <la vera comprensione dell’entanglement potrà ottenersi solamente quando saremo in grado di dare una risposta alla domanda posta a suo tempo da John Archibald Wheeler [(Jacksonville, 1911 – Hightstown, 2008), allievo di Bohr] “Perché il quanto?”>. L’introduzione del ‘quanto’ nella fisica difatti stravolge tutto il modo di pensare e di conoscere la realtà o, se si vogliono utilizzare i termini di Kant, del noumeno e del fenomeno. Heisenberg afferma:” L’adattamento del nostro pensiero e del nostro linguaggio ai fenomeni della fisica atomica è tuttavia collegato, come nella teoria della relatività, a delle grandi difficoltà. Nella teoria della relatività erano molto utili a questo adattamento le discussioni filosofiche dei primi tempi sui problemi dello spazio e del tempo. In modo simile nella fisica atomica si può trar giovamento dalle discussioni, fondamentali per tutta la teoria della conoscenza, sulle difficoltà che sono collegate con la separazione del mondo in soggetto e oggetto” [7].
Nuovi scenari imprevedibili saranno aperti infatti dall’ipotesi del ‘quanto’ di Planck non solo sulla conoscenza della luce e della materia, ma addirittura sulla struttura stessa dello spazio-tempo.