percorso di Marco Capogni
La relatività generale, basandosi su quanto scoperto nella relatività ristretta e suggellato dalla equazione (1), porta - come conseguenza estrema della teoria - a definire il buco nero (black hole) (Fig. 27): un corpo che ha una massa \(M_\odot\) tale da generare una gravità così intensa che nulla può sfuggirgli, nemmeno la luce stessa. In Fig. 28 un’analogia tra il buco nero e il gorgo di un fiume: il pesciolino nella figura rappresenta lo spazio-tempo; per una distanza dal centro del gorgo (“singolarità” presente nel buco nero) inferiore al raggio del suo bordo (“orizzonte degli eventi”) tutto viene inghiottito.

fig. 27, Buco Nero e orizzonte degli eventi (schematizzato con la linea tratteggiata in bianco)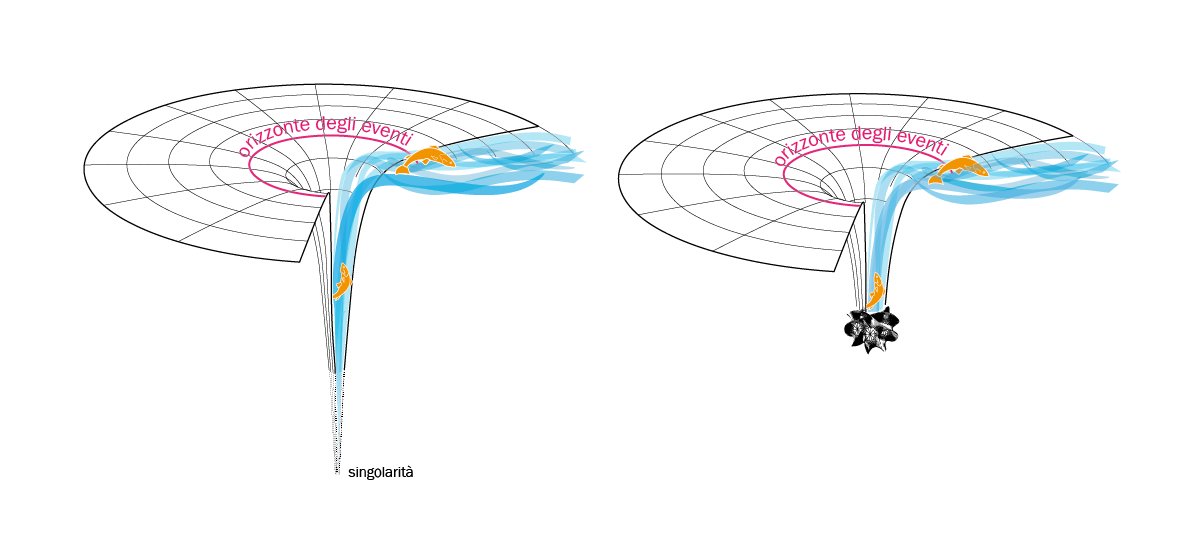
fig. 28, Effetto dell’orizzonte degli eventi sui raggi di luce (©Asimmetrie INFN- cuicchio)
Per stimare la dimensione dell’orizzonte degli eventi occorre imporre che la velocità di fuga dalla gravità di \(M_\odot\) sia pari a \(c\) [26], da cui si ottiene che la massa del corpo deve essere contenuta entro un raggio \(r_s\), noto come raggio di Schwarzschild, dato da \[r_s=\frac{2GM_\odot}{c^2} ~(7)\] Il raggio di Schwarzschild determina dunque la regione dello spazio-tempo, delimitata dall’ orizzonte degli eventi, in cui si è prodotto un buco nero al cui interno esiste una singolarità per cui tutte le leggi della fisica a noi note perdono senso (si creano di fatti quantità divergenti o infinite nelle equazioni stesse).
Nel provare a combinare la meccanica quantistica con la relatività generale ci si trova subito di fronte a limitazioni imposte dal principio di indeterminazione, introdotto dall’una teoria, e al fenomeno del buco nero, introdotto dall’altra teoria. Sono proprio queste limitazioni che portano a definire dei valori limiti inferiori per la misura dello spazio e del tempo. Infatti, il concetto stesso di ‘misura’ dello spazio, nella sua accezione fisica, significa proprio poter localizzare con estrema precisione in esso una particella di massa \(m\), ma ciò comporta, per il principio di indeterminazione, una quantità di moto infinita, ovvero un’energia infinita. Un’energia infinita determina, per la relatività generale, una curvatura dello spazio così elevata che la particella cade nel buco nero da lei stessa generato. Per evitare tutto ciò, che renderebbe insensata qualunque misura dello spazio fisico (portando lo stesso a collassare in un buco nero), occorre individuare la minima dimensione spaziale che si può ‘misurare’ utilizzando una particella di massa \(m\). Considerando l’equazione (3), a \(m\) si può associare una lunghezza d’onda \(λ_c=h/mc\), nota anche come “lunghezza d’onda Compton” della particella, che è equivalente alla lunghezza d’onda di un fotone che ha energia \(E=mc^2\), data dalla (1), ovvero equivalente alla massa a riposo della particella.
Escludere problemi di energia infinita significa imporre che \(λ_c\) non sia nulla ed ammetta un limite inferiore; significa dunque ammettere un limite superiore alla massa della particella stessa. Il limite su \(λ_c\) (imposto per evitare che la particella collassi nel suo stesso buco nero) va cercato ponendo \(λ_c=r_s\) da cui si ricava il valore massimo ammissibile per \(m=√(hc/2G)\), oltre il quale la particella sprofonda irreversibilmente appunto nel buco nero che essa genera. Tale massa, eccetto un fattore numerico pari a \(√π\), è proprio la massa di Planck ed è associata a un raggio di Schwarzschild pari a \(√(2Gh/c^3 )\), che a sua volta, eccetto un fattore numerico pari a \(√4π\), rappresenta la lunghezza di Planck, \( l_p\). Tale lunghezza fornisce quindi la dimensione di una massa di Planck oltre cui una particella di massa \(m\) collassa nel buco nero generato da essa stessa.
L’esistenza di una lunghezza minimale \(l_p \) (al di sotto della quale non si può scendere senza evitare che lo spazio stesso collassi in un buco nero) impone anche l’esistenza di un tempo minimale \(t_p = l_p/c\), al di sotto del quale non si può scendere e che rappresenta il tempo impiegato da un fotone per percorrere una distanza di Planck: il tempo di Planck. Le due grandezze \(l_p\) e \(t_p\) sono dunque i limiti inferiori dello spazio-tempo al di sotto dei quali nessuna struttura fisica del mondo, che le nostre equazioni sanno descrivere, ha senso.
E’ quindi chiaro che le unità di misura di Planck - che mettono insieme \(c\) (costante principale della teoria della relatività ristretta), \(G\) (costante principale della teoria della relatività generale) e \(h\) (costante principale della meccanica quantistica) - si prestano a descrivere particolarmente bene situazioni in cui gravità e meccanica quantistica si confrontano come le singolarità dello spazio-tempo presenti nei buchi neri o all’epoca del Big Bang (il grande inizio dell’Universo) o del Big Crunch (la grande implosione, se mai ci sarà una fine di tutto dovuto ad un collasso dell’Universo su se stesso per effetto della forza di gravità).
Non può però mancare nella descrizione delle unità di Planck una riflessione su una branca della scienza, che ha dato proprio il motivo a Planck di introdurre nella descrizione della natura il suo ‘quanto di azione’: la termodinamica. Si deve infatti a Jacob Bekenstein (Città del Messico, 1947 – Helsinki, 2015) e Stephen Hawking (Oxford, 1942 – Cambridge, 2018) il primo approccio termodinamico alla descrizione di un buco nero. Essi definirono l’entropia, \(S_{BH}\), di un buco nero mediante l’area \(A\) (pari a \(πr_s^2 \) ) dell’orizzonte degli eventi misurata in unità di area di Planck, \(l_p^2\), secondo la formula:
\[ S_{BH}=\frac{K_B A}{4l_p^2} ~(8)\]
dove \(K_B\) è la costante di Ludwig Eduard Boltzmann (Vienna, 1844 – Duino, 1906) e pari a circa 1,3807 10-23 JK-1 ; (notare, per inciso, che nella formula (8) il pedice usato \(BH\) può intendersi, quasi per ironia della sorte, tanto Bekenstein-Hawking quanto Black-Hole).
L’equazione (8) si presenta come la prima vera formula che mette insieme, mediante \(l_p\), la costante di Planck \(h\) con la costante di Newton \(G\). Ciò significa che tale entropia è un primo effetto di una connessione tra la gravità e la meccanica quantistica, studiata nella teoria della gravità quantistica.

